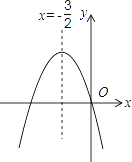Question

【题目】已知关于x的一元二次方程mx2+（3m+1）x+3=0．

（1）求证：该方程有两个实数根；

（2）如果抛物线y=mx2+（3m+1）x+3与x轴交于A、B两个整数点（点A在点B左侧），且m为正整数，求此抛物线的表达式；

（3）在（2）的条件下，抛物线y=mx2+（3m+1）x+3与y轴交于点C，点B关于y轴的对称点为D，设此抛物线在﹣3≤x≤﹣之间的部分为图象G，如果图象G向右平移n（n＞0）个单位长度后与直线CD有公共点，求n的取值范围．

Answer 1

【答案】（1）证明见解析；（2）y=x2+4x+3；（3）≤n≤4；

【解析】

（1）先求出根的判别式△，判断△的取值范围，即可得证；

（2）根据求根公式表示出两根，由题意，求出m的值，可得抛物线的解析式；

（3）点求出点A，B，C，D的坐标，根据待定系数法求出直线CD的解析式，设平移后，点A，E的对应点分别为A′（﹣3+n，0），E′（﹣+n，），根据点在直线上，求出取值范围即可．

（1）由根的判别式，可得：△=（3m+1）2﹣4×m×3=（3m﹣1）2．

∵（3m﹣1）2≥0，∴△≥0，∴原方程有两个实数根；

（2）令y=0，那么mx2+（3m+1）x+3=0，解得：x1=﹣3，x2=﹣．

∵抛物线与x轴两个交点的横坐标均为整数，且m为正整数，∴m=1，∴抛物线的解析式为：y=x2+4x+3；

（3）如图，∵当x=0时，y=3，∴C（0，3）．

∵当y=0时，x1=﹣3，x2=﹣1．

又∵点A在点B的左侧，∴A（﹣3，0），B（﹣1，0）．

∵点D与点B关于y轴对称，∴D（1，0），设直线CD的解析式为：y=kx+b，∴，解得：，∴直线CD的表达式为：y=﹣3x+3．

又∵当x=﹣时，y=，∴点E（﹣），∴平移后，点A，E的对应点分别为A′（﹣3+n，0），E′（﹣+n，），当直线y=﹣3x+3经过点A′（﹣3+n，0）时，得：﹣3（﹣3+n）+3=0，解得：n=4，当直线y=﹣3x+3经过点E′（﹣+n，），时，得：﹣3（﹣+n）+3=，解得：n=，∴n的取值范围是≤n≤4．