题目内容
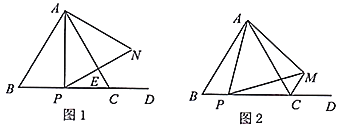
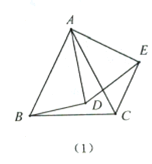
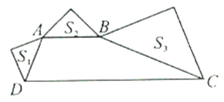
【题目】如图,在四边形![]() 中,
中,![]() ,以
,以![]() 为斜边均向形外作等腰直角三角形,其面积分别是
为斜边均向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】4
【解析】
过点B作BM∥AD,根据AB∥CD,求证四边形ADMB是平行四边形,再利用∠ADC+∠BCD=90°,求证△MBC为直角三角形,再利用勾股定理得出MC2=MB2+BC2,根据等腰直角三角形的性质分别求出三个等腰直角三角形的面积,计算即可.
解:过点B作BM∥AD交CD于M,

∵AB∥CD,
∴四边形ADMB是平行四边形,
∴AB=DM,AD=BM,
∵∠ADC+∠BCD=90°,
∴∠BMC+∠BCM=90°,即∠MBC=90°,
∴MC2=MB2+BC2,
∵△ADE是等腰直角三角形,
∴AE2+DE2=AD2,
∴AE2=DE2=![]() AD2,
AD2,
∴S1=![]() ×AE×DE=
×AE×DE=![]() AE2=
AE2=![]() AD2,,
AD2,,
同理:S2=![]() AB2,S3=
AB2,S3=![]() BC2,
BC2,
S1+S3=![]() AD2+
AD2+![]() BC2=
BC2=![]() BM2+
BM2+![]() BC2=
BC2=![]() MC2,
MC2,
∵CD=3AB,
∴MC=2AB,
∴S1+S3 =![]() ×(2AB)2= AB2,
×(2AB)2= AB2,
∴S1+S3=4S2,即k=4,
故答案为:4.

【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.