题目内容
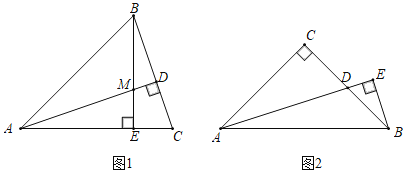
【题目】(1)如图1,在△ABC中,AB=AC,∠BAC=45°.△ABC的高AD、BE相交于点M.求证:AM=2CD;
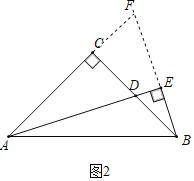
(2)如图2,在Rt△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,过点B作BE⊥AD,交AD的延长线于点 E.若AD=3,则BE= .
【答案】(1)详见解析;(2)1.5.
【解析】
(1)根据全等三角形的判定和性质定理以及等腰三角形的性质定理,即可得到结论;
(2)延长BE、AC交于F点,首先利用三角形内角和定理计算出∠F=∠ABF,进而得到AF=AB,再根据等腰三角形的性质可得BE=![]() BF,然后证明△ADC≌△BFC,可得BF=AD,进而得到BE=
BF,然后证明△ADC≌△BFC,可得BF=AD,进而得到BE=![]() AD,即可求解.
AD,即可求解.
(1)在△ABC中,
∵∠BAC=45°,BE⊥AC,
∴AE=BE,
∵AD⊥BC,
∴∠EAM=90°-∠C=∠EBC,
在△AEM和△BEC中,
∵ ,
,
∴△AEM≌△BEC(ASA),
∴AM=BC,
∵AB=AC,AD⊥BC,
∴BD=CD,
∴BC=2CD,
∴AM=2CD;
(2)延长BE、AC交于F点,
∵BE⊥EA,
∴∠AEF=∠AEB=90°.
∵AD平分∠BAC,
∴∠FAE=∠BAE,
∴∠F=∠ABE,
∴AF=AB,
∵BE⊥EA,
∴BE=EF=![]() BF,
BF,
∵△ABC中,AC=BC,∠C=90°,
∴∠CAB=45°,
∴∠AFE=(180°﹣45°)÷2=67.5°,∠FAE=45°÷2=22.5°,
∴∠CDA=67.5°,
∵在△ADC和△BFC中,
∵ ,
,
∴△ADC≌△BFC(AAS),
∴BF=AD,
∴BE=![]() AD=1.5,
AD=1.5,
故答案为:1.5.

【题目】某公司招聘一名员工,现有甲、乙两人竞聘,公司聘请了3位专家和4位群众代表组成评审组,评审组对两人竟聘演讲进行现场打分,记分采用100分制,其得分如下表:
评委(序号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙两位竞聘者得分的中位数分别是多少
(2)计算甲、乙两位应聘者平均得分,从平均得分看应该录用谁(结果保留一位小数)
(3)现知道1、2、3号评委为专家评委,4、5、6、7号评委为群众评委,如果对专家评委组与群众评委组的平均分数分别赋子适当的权,那么对专家评委组赋的权至少为多少时,甲的平均得分比乙的平均得分多0.5分及以上