题目内容
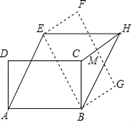
【题目】如图,矩形ABCD中,AB=3,AD=![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
【答案】D
【解析】
由旋转的性质得到AB=BE,根据菱形的性质得到AE=AB,推出△ABE是等边三角形,得到AB=3,AD=![]() ,根据三角函数的定义得到∠BAC=30°,求得AC⊥BE,推出C在对角线AH上,得到A,C,H共线,于是得到结论.
,根据三角函数的定义得到∠BAC=30°,求得AC⊥BE,推出C在对角线AH上,得到A,C,H共线,于是得到结论.
如图,连接AC交BE于点O,
∵将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,
∴AB=BE,
∵四边形AEHB为菱形,
∴AE=AB,
∴AB=AE=BE,
∴△ABE是等边三角形,
∵AB=3,AD=![]() ,
,
∴tan∠CAB=![]() ,
,
∴∠BAC=30°,
∴AC⊥BE,
∴C在对角线AH上,
∴A,C,H共线,
∴AO=OH=![]() AB=
AB=![]() ,
,
∵OC=![]() BC=
BC=![]() ,
,
∵∠COB=∠OBG=∠G=90°,
∴四边形OBGM是矩形,
∴OM=BG=BC=![]() ,
,
∴HM=OH﹣OM=![]() ,
,
故选D.

练习册系列答案
相关题目
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2