Question

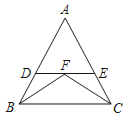
【题目】如图，△ABC中，AB＝AC，小聪同学利用直尺和圆规完成了如下操作：

①作∠BAC的平分线AM交BC于点D；

②作边AB的垂直平分线EF，EF与AM相交于点P；

③连接PB，PC．

请你观察图形解答下列问题：

（1）线段PA，PB，PC之间的数量关系是　 　；

（2）若∠ABC＝70°，求∠BPC的度数．

Answer 1

【答案】（1）PA＝PB＝PC；（2）∠BPC＝80°．

【解析】

（1）根据线段的垂直平分线的性质可得：PA=PB=PC；

（2）根据等腰三角形的性质得：∠ABC=∠ACB=70°，由三角形的内角和得：∠BAC=40°，由角平分线定义得：∠BAD=∠CAD=20°，最后利用三角形外角的性质可得结论．

（1）PA=PB=PC．理由如下：

∵AB=AC，AM平分∠BAC，∴AD是BC的垂直平分线，∴PB=PC．

∵EP是AB的垂直平分线，∴PA=PB，∴PA=PB=PC．

故答案为：PA=PB=PC；

（2）∵AB=AC，∴∠ABC=∠ACB=70°，∴∠BAC=180°﹣2×70°=40°．

∵AM平分∠BAC，∴∠BAD=∠CAD=20°．

∵PA=PB=PC，∴∠ABP=∠BAP=∠ACP=∠CAP=20°，∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°．