题目内容
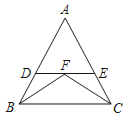
【题目】如图，∠ABC和∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于D，交AC于E，下列结论正确的是（ ）
①BD＝CE②△BDF，△CEF都是等腰三角形③BD+CE＝DE④△ADE的周长为AB+AC．
A.①②B.③④C.①②③D.②③④
【答案】D
【解析】
①②根据平分线的性质、平行线的性质，借助于等量代换可求出∠DBF=∠DFB，即△BDF是等腰三角形，同理△CEF都是等腰三角形；③利用等腰三角形的性质即可证明;由④可得△ADE的周长为AB+AC；无法判断；
解：∵BF平分∠ABC，
∴∠ABF＝∠CBF，
∵DE∥BC，
∴∠CBF＝∠BFD，
∴∠ABF＝∠BFD，
∴BD＝FD，
同理可得CE＝CF，
∴△BDF，△CEF都是等腰三角形；①不正确，②正确；
∴BD+CE＝FD+FE＝DE，③正确；
△ADE的周长＝AD+FD+FE+AE＝AD+BD+CE+AE＝AB+AC，④正确
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
