题目内容
【题目】(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC.求证:△ABD≌△ACE;
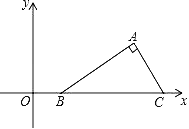
(2)探索:如图2,在Rt△ABC与Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;
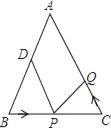
(3)应用:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=6,CD=2,求AD的长.

【答案】(1)见解析;(2)2AD2=BD2+CD2,理由见解析;(3)4.
【解析】
(1)先利用等腰直角三角形的性质推出∠BAD=∠CAE,然后用边角边证明△BAD≌△CAE即可;
(2)连接EC,先用边角边证明△BAD≌△CAE,得到∠B=∠ACE=45°,进而推出∠BCE=90°,由勾股定理可得DE2=CE2+CD2,然后再由DE=![]() AD可得出结论;
AD可得出结论;
(3)将AD绕点A逆时针旋转90°至AG,连接CG、DG,易得△DAG是等腰直角三角形,同理可证△BAD≌△CAG,然后推出DG=4![]() ,即可得结果.
,即可得结果.
解:(1)在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
 ,
,
∴△BAD≌△CAE(SAS),
(2)结论:2AD2=BD2+CD2,
理由是:如图2中,连接EC.

∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∵ ,
,
∵△BAD≌△CAE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
∴DE2=CE2+CD2,
∵AD=AE,∠DAE=90°,
∴DE=![]() AD,
AD,
∴2AD2=BD2+CD2;
(3)如图3,将AD绕点A逆时针旋转90°至AG,连接CG、DG,

则△DAG是等腰直角三角形,
∴∠ADG=45°,
∵∠ADC=45°,
∴∠GDC=90°,
同理得:△BAD≌△CAG,
∴CG=BD=6,
Rt△CGD中,∵CD=2,
∴DG=4![]() ,
,
∵△DAG是等腰直角三角形,
∴AD=AG=4.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案