��Ŀ����
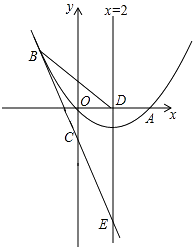
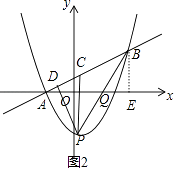
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y= ![]() x+1��������y=ax2+bx��3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��AB�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB���C����PD��AB�ڵ�D
x+1��������y=ax2+bx��3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��AB�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB���C����PD��AB�ڵ�D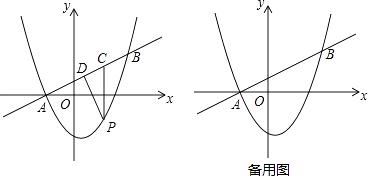
��1�����������ߵĽ���ʽ������sin��ACP��ֵ
��2�����P�ĺ�����Ϊm
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ���������������������֮��Ϊ9��10ʱ��mֵ��
���Ƿ�����ʺϵ�mֵ��ʹ��PCD���PBD���ƣ������ڣ�ֱ��д��mֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��
�⣺�ٵ�y=0ʱ�� ![]() x+1=0�����x=��2����A����2��0����
x+1=0�����x=��2����A����2��0����
��y=3ʱ�� ![]() x+1=3�����x=4����B��4��3����
x+1=3�����x=4����B��4��3����
��A����2��0����B��4��3������y=ax2+bx��3�� ![]() �����
����� 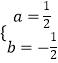 ��
��
�������ߵĽ���ʽΪy= ![]() x2��
x2�� ![]() x��3��
x��3��
�ڹ�B��BE��x���ڵ�E����ͼ1��
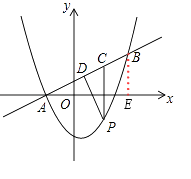
AE=4������2��=6��AB= ![]() =3
=3 ![]() ��
��
��Rt��ABE��sin��ABE= ![]() =
= ![]() =
= ![]() ��
��
��PC��BE��
��sin��ACP=sin��ABE= ![]() ��
��
��2��
�⣺��P��m�� ![]() m2��
m2�� ![]() m��3������C��m��
m��3������C��m�� ![]() m+1����BM=4��m��
m+1����BM=4��m��
��PC= ![]() m+1����
m+1���� ![]() m2��
m2�� ![]() m��3��=��
m��3��=�� ![]() m2+m+4��
m2+m+4��
��sin��ACP= ![]() =
= ![]() ��
��
��PD=�� ![]() m2+
m2+ ![]() m+
m+ ![]() =��
=�� ![]() ��m��1��2+
��m��1��2+ ![]() ��
��
��m=1ʱ���߶�PD�������ֵΪ ![]() ��
��
����BM��PC����PC���ӳ����ڵ�M����DN��PC�ڵ�N����ͼ��
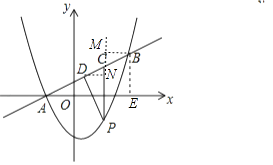
��sinP=sin��BAE= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��DN= ![]() ��
�� ![]() m2+
m2+ ![]() m+
m+ ![]() ��=��
��=�� ![]() m2+
m2+ ![]() m+
m+ ![]() ��
��
��DN��BM��
�� ![]() =
= ![]() ��
��
���߶�PC�ѡ�PDB�ֳ����������ε����֮��Ϊ9��10��
�൱ ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
������2m2��13m+20=0�����m1= ![]() ��m2=4����ȥ����
��m2=4����ȥ����
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
������9m2��68m+128=0�����m1= ![]() ��m2=4����ȥ����
��m2=4����ȥ����
����������m��ֵΪ ![]() ��
�� ![]() ��
��
�۴��ڣ�
��ͼ2������PB��x����Q��
�ߡ�PDC=��BDP��
�൱DPC=��DBPʱ����DPC�ס�DBP��
����DPC=��BAE��
���BAE=��ABP��
��QA=QB��
��Q��t��0������QA=QB=t+2��EQ=4��t��
��Rt��BQE����4��t��2+32=t2�����t= ![]() ����Q��
����Q�� ![]() ��0����
��0����
��ֱ��BQ�Ľ���ʽΪy=px+q��
��B��4��3����Q�� ![]() ��0�������
��0������� 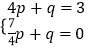 �����
����� 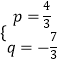 ��
��
��ֱ��BQ�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
�ⷽ���� 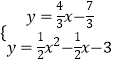 ��
�� ![]() ��
�� 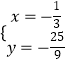 ��
��
��P���� ![]() ����
���� ![]() ����
����
��m=�� ![]() ��
��
����������1������ֱ�߽���ʽ�����A��B��������꣬���������߽���ʽ�����a��b��ֵ�������������߽���ʽ���ڹ�B��BE��x���ڵ�E����Rt��ABE�п����sin��ABE��������sin��ACP����2������m�ɱ�ʾ��C�����꣬��ɱ�ʾ��PC�ij�������������ֵ�ɱ�ʾ��PD�ij������ö��κ��������ʿ���������ֵ������BM��PC����PC���ӳ����ڵ�M����DN��PC�ڵ�N�������m��ʾDN��BM��������ıȵõ�DC��BC�ıȣ�Ȼ���������Ʊȿɵõ�m�ķ��̣������m��ֵ������ͼ2������PB��x����Q��ֻ�е�DPC=��DBPʱ����DPC�ס�DBP�����ǿ�֤��QA=QB����Q��t��0������QA=QB=t+2��EQ=4��t�����ù��ɶ����õ���4��t��2+32=t2 �� ���t= ![]() ����Q��
����Q�� ![]() ��0���������ô���ϵ�������ֱ��BQ�Ľ���ʽΪy=
��0���������ô���ϵ�������ֱ��BQ�Ľ���ʽΪy= ![]() x��
x�� ![]() ��Ȼ��ⷽ����
��Ȼ��ⷽ���� 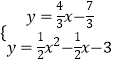 ��P�����꣬�Ӷ��õ�m��ֵ��
��P�����꣬�Ӷ��õ�m��ֵ��

 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�����Ŀ��ij������ҵ�������м�������15�ˣ�������Ϊ�˺����ƶ���Ʒ��ÿ���������ͳ������15��ij�µļӹ����������
ÿ�˼ӹ�������� | 540 | 450 | 300 | 240 | 210 | 120 |
���� | 1 | 1 | 2 | 6 | 3 | 2 |
(1)д����15�˸��¼ӹ��������ƽ��������λ����������
(2)���������������˰�ÿλ���˵��¼ӹ����������Ϊ260������Ϊ��������Ƿ������Ϊʲô��