��Ŀ����
����Ŀ����ͼ����֪�����߾���ԭ��o��x����һ��A��4��0���������߶���ΪE�����ĶԳ�����x�ύ�ڵ�D��ֱ��y=��2x��1������������һ��B����2��m������y�ύ�ڵ�C���������ߵĶԳ��ύ�ڵ�F��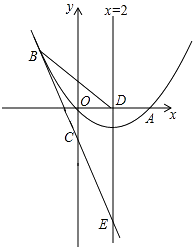
��1����m��ֵ���������߶�Ӧ�Ľ���ʽ��
��2��P��x��y�����������ϵ�һ�㣬��S��ADP=S��ADC �� ������з��������ĵ�P�����ꣻ
��3����Q��ƽ��������һ�㣬��M�ӵ�F�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������M���˶�ʱ��Ϊt�룬�Ƿ���ʹ��Q��A��E��M�ĵ�Ϊ������ı��������Σ����ܣ���ֱ��д����M���˶�ʱ��t��ֵ�������ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�B����2��m����ֱ��y=��2x��1��
��m=��2������2����1=4��1=3��
���ԣ���B����2��3����
�֡������߾���ԭ��O��
���������ߵĽ���ʽΪy=ax2+bx��
�ߵ�B����2��3����A��4��0�����������ϣ�
�� ![]() ��
��
��ã� 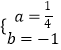 ��
��
�������ߵĽ���ʽΪy= ![]() x2��x
x2��x
��2��
�⣺��P��x��y�����������ϵ�һ�㣬
��P��x�� ![]() x2��x����
x2��x����
��S��ADP=S��ADC��
��S��ADC= ![]() ADOC��S��ADP=
ADOC��S��ADP= ![]() AD|y|
AD|y|
�֡ߵ�C��ֱ��y=��2x��1��y�ύ�㣬
��C��0����1����
��OC=1��
��| ![]() x2��x|=
x2��x|= ![]() ����
���� ![]() x2��x=1��
x2��x=1�� ![]() x2��x=��1��
x2��x=��1��
��ã�x1=2+2 ![]() ��x2=2��2
��x2=2��2 ![]() ��x3=x4=2��
��x3=x4=2��
���P������Ϊ P1��2+2 ![]() ��1����P2��2��2
��1����P2��2��2 ![]() ��1����P3��2����1��
��1����P3��2����1��
��3��
�⣺���ۣ����ڣ�
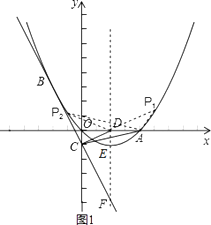
�������ߵĽ���ʽΪy= ![]() x2��x��
x2��x��
�ඥ��E��2����1�����Գ���Ϊx=2��
��F��ֱ��y=��2x��1��Գ���x=2�Ľ��㣬
��F��2����5����DF=5��
�֡�A��4��0����
��AE= ![]() ��
��
����ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�
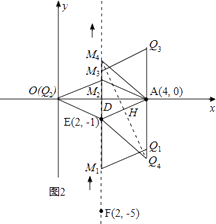
������AEM1Q1��
�ߴ�ʱEM1=AE= ![]() ��
��
��M1F=DF��DE��DM1=4�� ![]() ��
��
��t1=4�� ![]() ��
��
������AEOM2��
�ߴ�ʱDM2=DE=1��
��M2F=DF+DM2=6��
��t2=6��
������AEM3Q3��
�ߴ�ʱEM3=AE= ![]() ��
��
��DM3=EM3��DE= ![]() ��1��
��1��
��M3F=DM3+DF=�� ![]() ��1��+5=4+
��1��+5=4+ ![]() ��
��
��t3=4+ ![]() ��
��
������AM4EQ4��
��ʱAEΪ���εĶԽ��ߣ���Խ���AE��M4Q4���ڵ�H����AE��M4Q4��
����֪��AED�ס�M4EH��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ����M4E=2.5��
����M4E=2.5��
��DM4=M4E��DE=2.5��1=1.5��
��M4F=DM4+DF=1.5+5=6.5��
��t4=6.5��
�������������ڵ�M����Q��ʹ����Q��A��E��M�ĵ�Ϊ������ı��������Σ�ʱ��t��ֵΪ��t1=4�� ![]() ��t2=6��t3=4+
��t2=6��t3=4+ ![]() ��t4=6.5��
��t4=6.5��
����������1�����������B�������m��ֵ��Ȼ�����ô���ϵ������������ߵĽ���ʽ����2����ADP���ADC�й�ͬ�ĵױ�AD����Ϊ�����ȣ�����AD���ϵĸ���ȣ���Ϊ1���Ӷ��õ���P��������Ϊ1�������������ߵĽ���ʽ�����P�������ꣻ��3������ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�ע�ⲻҪ©�⣮���ÿһ�����Σ��ֱ���м��㣬����߶�MF�ij��ȣ��Ӷ��õ��˶�ʱ��t��ֵ��

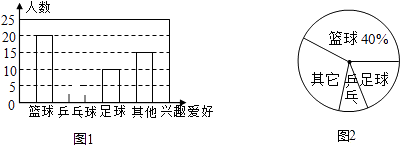
����Ŀ�����ؿ�����ij���ӵ�·�峧������ɽ��ѧ��Ӧ���ҵ������Ƹ��˾ְԱ����ӦƸ�ߵ�רҵ֪ʶ��Ӣ��ˮƽ���μ����ʵ�������Ż��������в��Ի�ɹ��϶�������ĵ÷����ֶ�Ϊ100�֣�����ķ����ֱ�5��3��2�ı�������ÿ�˵�����ܷ֣���4λӦƸ�ߵĵ÷����±���ʾ��
| רҵ֪ʶ | Ӣ��ˮƽ | �μ����ʵ���� ���Ż�� |
�� | 85 | 85 | 90 |
�� | 85 | 85 | 70 |
�� | 80 | 90 | 70 |
�� | 90 | 90 | 50 |
��1���ֱ����4λӦƸ�ߵ��ܷ֣�
��2���������ˡ�רҵ֪ʶ����ƽ����Ϊ85�֣�����Ϊ12.5�����ˡ�Ӣ��ˮƽ����ƽ����Ϊ87.5�֣�����Ϊ6.25������������ˡ��μ����ʵ�������Ż�ȡ���ƽ���ּ����
��3��������1���ͣ�2���е��й����ݣ���Դ�ѧ��ӦƸ���кν��飿
����Ŀ��ij�̳���Ӫij��Ʒ�Ƶ���ߣ�����ʱ�ĵ�����30Ԫ�������г����飺��һ��ʱ���ڣ����۵�����40Ԫʱ����������600���������۵���ÿ��1Ԫ���ͻ����۳�10����ߣ�
��1�����������Ʒ����ߵ����۵���ΪxԪ��x��40��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ����������wԪ�����ѽ����д�ڱ����У�
���۵��ۣ�Ԫ�� | x |
������y������ | |
������������w��Ԫ�� |
��2���ڣ�1���������£����̳������10000Ԫ�����������������۵���xӦ��Ϊ����Ԫ��
��3���ڣ�1���������£�����߳��涨��Ʒ��������۵��۲�����44Ԫ�����̳�Ҫ��ɲ�����540���������������̳����۸�Ʒ�����õ���������Ƕ��٣�