题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,﹣4).
(1)求该二次函数的解析式;
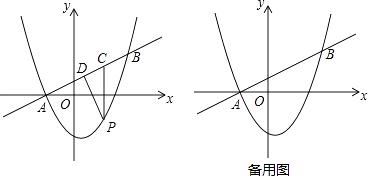
(2)A、B为直线y=﹣2x﹣6上两动点,且距离为2,点C为二次函数图象上的动点,当点C运动到何处时△ABC的面积最小?求出此时点C的坐标及△ABC面积的最小值.
【答案】
(1)
解:∵点(1,0),(5,0),(3,﹣4)在抛物线上,
∴ 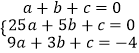 ,
,
解得 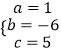 .
.
∴二次函数的解析式为:y=x2﹣6x+5.
(2)
解:

设直线y=﹣2x﹣6与x轴,y轴分别交于点M,点N,
令x=0,得y=﹣6;令y=0,得x=﹣3
∴M(﹣3,0),N(0,﹣6),
∴OM=3,ON=6,由勾股定理得:MN=3 ![]() ,
,
∴tan∠MNO= ![]() =
= ![]() ,sin∠MNO=
,sin∠MNO= ![]() =
= ![]() .
.
设点C坐标为(x,y),则y=x2﹣6x+5.
过点C作CD⊥y轴于点D,则CD=x,OD=﹣y,DN=6+y.
过点C作直线y=﹣2x﹣6的垂线,垂足为E,交y轴于点F,
在Rt△CDF中,DF=CDtan∠MNO= ![]() x,CF=
x,CF= ![]() =
= ![]() =
= ![]() x.
x.
∴FN=DN﹣DF=6+y﹣ ![]() x.
x.
在Rt△EFN中,EF=FNsin∠MNO= ![]() (6+y﹣
(6+y﹣ ![]() x).
x).
∴CE=CF+EF= ![]() x+
x+ ![]() (6+y﹣
(6+y﹣ ![]() x),
x),
∵C(x,y)在抛物线上,∴y=x2﹣6x+5,代入上式整理得:
CE= ![]() (x2﹣4x+11)=
(x2﹣4x+11)= ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,
,
∴当x=2时,CE有最小值,最小值为 ![]() .
.
当x=2时,y=x2﹣6x+5=﹣3,∴C(2,﹣3).
△ABC的最小面积为: ![]() ABCE=
ABCE= ![]() ×2×
×2× ![]() =
= ![]() .
.
∴当C点坐标为(2,﹣3)时,△ABC的面积最小,面积的最小值为 ![]() .
.
【解析】(1)利用待定系数法求出抛物线的解析式;(2)△ABC的底边AB长度为2,是定值,因此当AB边上的高最小时,△ABC的面积最小.如解答图所示,由点C向直线y=﹣2x﹣6作垂线,利用三角函数(或相似三角形)求出高CE的表达式,根据表达式求出CE的最小值,这样问题得解.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】某校九年级为建立学习兴趣小组,对语文、数学、英语、物理、化学、思想品德、历史、综合共八个科目的喜欢情况进行问卷调查(每人只选一项),下表是随机抽取部分学生的问卷进行统计的结果:
科目 | 语文 | 数学 | 英语 | 物理 | 化学 | 思想品德 | 历史 | 综合 |
人数 | 6 | 10 | 11 | 12 | 10 | 9 | 8 | 14 |

根据表中信息,解答下列问题:
(1)本次随机抽查的学生共有人;
(2)本次随机抽查的学生中,喜欢科目的人数最多;
(3)根据上表中的数据补全条形统计图;
(4)如果该校九年级有600名学生,那么估计该校九年级喜欢综合科目的学生有多少人.