Question

【题目】如图，AB是⊙O的弦，OH⊥AB于点H，点P是优弧上一点，若AB=2 ，OH=1，则∠APB的度数是 ．

Answer 1

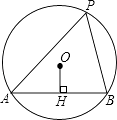
【答案】60°
【解析】解：连接OA，OB，
∵OH⊥AB，AB=2 ，
∴AH= AB= ，
∵OH=1，
∴tan∠AOH = ．
∴∠AOH=60°，
∴∠AOB=2∠AOH=120°，
∴∠APB= ∠AOB= ×120°=60°．
所以答案是：60°．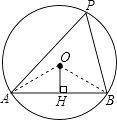

【考点精析】认真审题，首先需要了解垂径定理(垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧)，还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键．