题目内容
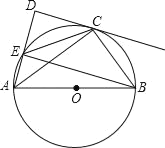
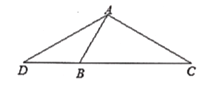
【题目】如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.
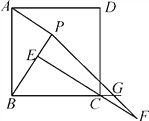
(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
【答案】(1)四边形ABCD为正方形.证明见解析;(2)∠BGP=45°
【解析】试题分析:(1)由四边形ABCD为矩形可得![]() 易得
易得![]() 由AP⊥BP,可得
由AP⊥BP,可得![]() 易得∠PBC=∠PAB,由AAS定理可得△ABP≌△BCE,由全等三角形的性质可得AB=BC,易得结论;
易得∠PBC=∠PAB,由AAS定理可得△ABP≌△BCE,由全等三角形的性质可得AB=BC,易得结论;
(2)连接AC,由△ABP≌△BCE,易得![]() 又
又![]() 可得
可得![]() 易得四边形
易得四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 由四边形
由四边形![]() 是正方形,
是正方形,![]() 是对角线,可得
是对角线,可得![]()
试题解析:(1)四边形ABCD为正方形。
∵四边形ABCD是矩形,
![]() 即
即![]()
∵AP⊥BP,
![]()
∴∠PBC=∠PAB,
∵CE⊥BP,
![]()
在△ABP与△BCE中,
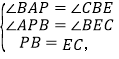
∴△ABP≌△BCE,
∴AB=BC,
∴矩形ABCD为正方形;
(2)连接AC,
∵△ABP≌△BCE,
∴AP=BE,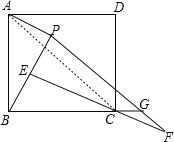
∵BE=CF,
∴AP=CF,
∵AP⊥BP,CE⊥BP,
∴AP∥CF,
∴四边形ACGP是平行四边形,
∴AC∥PF,
∴∠ACB=∠BGC,
∵四边形ABCD是正方形,AC是对角线,
![]()
∴![]()

【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.