题目内容
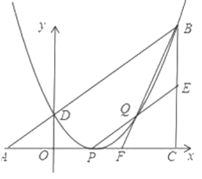
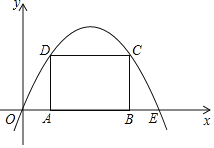
【题目】如图,一次函数 ![]() 与
与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与反比例函数
两点,与反比例函数![]() 相交于
相交于![]() 两点,分别过
两点,分别过![]() 两点作
两点作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() ,有下列四个结论:①
,有下列四个结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ∽
∽![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
A. 1B. 2C. 3D. 4
【答案】B
【解析】
试题设D(x,![]() ),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据面积相等,推出边EF上的高相等,推出CD∥EF,根据相似三角形的判定判断②即可;根据全等三角形的判定判断③即可;证出平行四边形BDFE和平行四边形ACEF,推出△ACF和△BDE的面积相等,根据三角形的面积公式推出BD=AC即可.
),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据面积相等,推出边EF上的高相等,推出CD∥EF,根据相似三角形的判定判断②即可;根据全等三角形的判定判断③即可;证出平行四边形BDFE和平行四边形ACEF,推出△ACF和△BDE的面积相等,根据三角形的面积公式推出BD=AC即可.
解:①设D(x,![]() ),则F(x,0),
),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是![]() ×
×![]() ×x=
×x=![]() k,
k,
同理可知:△CEF的面积是![]() k,
k,
∴△CEF的面积等于△DEF的面积,∴①正确;
②即△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
∴EF∥CD,
即AB∥EF,
∴△AOB∽△FOE,∴②正确;
③条件不足,无法证出两三角形全等的条件,∴③错误;
④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,∴④正确;
正确的有3个,
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目