题目内容
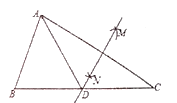
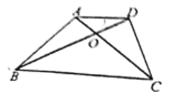
【题目】如图，已知梯形 ABCD 中，AD∥BC，对角线 AC、BD 相交于点O， △AOB 与△BOC 的面积分别为 4、8，则梯形ABCD 的面积等于___________
【答案】18
【解析】
首先△AOB与△BOC的面积分别为4和8，根据等高三角形的面积之比等于对应底边的比，即可求出AO：CO的值，由于AD∥BC，可得△OAD∽△COB，再根据相似三角形的面积之比等于相似比的平方即可求出△BOC的面积，进而求出梯形的面积．
解：∵△AOB 与△BOC 的面积分别为 4、8，
∴AO：CO=1：2
∵AD∥BC，
∴△OAD∽△COB，
∴
，
AO：CO=DO：BO=1：2
∴
，
，
∴梯形ABCD的面积为：4+8+4+2=18
故答案为：18．
练习册系列答案
阅读快车系列答案
相关题目
【题目】八年级（1）班张山同学利用所学函数知识，对函数y＝|x+2|﹣x﹣1进行了如下研究：
列表如下：
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | ||
Y | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 |
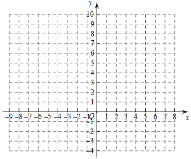
描点并连线（如下图）
（1）求表格中的m、n的值；
（2）在给出的坐标系中画出函数y＝|x+2|﹣x﹣1的图象；
（3）一次函数y＝﹣x+3的图象与函数y＝|x+2|﹣x﹣1的图象交点的坐标为 ．
