��Ŀ����
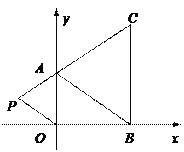
����Ŀ����ͼ��ֱ��l��y=x�� ![]() ��x�������ᡢy�Ḻ����ֱ��ཻ��A��C���㣬������y=
��x�������ᡢy�Ḻ����ֱ��ཻ��A��C���㣬������y= ![]() x2+bx+c������B����1��0���͵�C��
x2+bx+c������B����1��0���͵�C��
��1����գ�ֱ��д�������ߵĽ���ʽ����
��2����֪��Q��������y= ![]() x2+bx+c�ڵ��������ڵ�һ�����㣮
x2+bx+c�ڵ��������ڵ�һ�����㣮
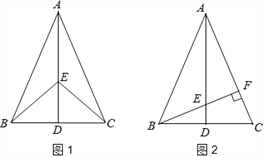
����ͼ������AQ��CQ�����Q�ĺ�����Ϊt����AQC�����ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
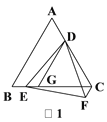
������BQ��AC�ڵ�D������BC����BDΪֱ������I���ֱ�BC��AB�ڵ�E��F������EF�����߶�EF����Сֵ����ֱ��д����ʱQ������꣮
���𰸡�
��1��y= ![]() x2��
x2�� ![]() x��
x�� ![]()
��2��
�⣺����QM��y�ύֱ��AC��M����ͼ�٣�
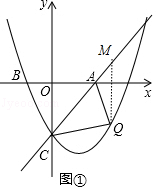
��Q��t�� ![]() t2��
t2�� ![]() t��
t�� ![]() ������M��t��t��
������M��t��t�� ![]() ����
����
��MQ=t�� ![]() ����
���� ![]() t2��
t2�� ![]() t��
t�� ![]() ��=��
��=�� ![]() t2+
t2+ ![]() t��
t��
��S=S��CMQ��S��AMQ= ![]() MQ1=��
MQ1=�� ![]() t2+
t2+ ![]() t=��
t=�� ![]() ��t��1��2+
��t��1��2+ ![]() ��
��
��t=1ʱ��S�����ֵ ![]() ��
��
������OE��OF����OH��EF��H����ͼ�ڣ���EH=FH��

��Rt��OBC����tan��OBC= ![]() =
= ![]() ��
��
���OBC=60�㣬
ͬ���ɵá�OAC=60�㣬AC=2OA=2��
���ABCΪ�ȱ������Σ�
�ߡ�EIF=2��EBF��
���EIF=120�㣬
���IEH=30�㣬
��Rt��IEH����cos��IEH= ![]() ��
��
��EH= ![]() IE��
IE��
��EF=2EH= ![]() IE��
IE��
��IE= ![]() BD
BD
��EF= ![]() BD��
BD��
��BD��ֵ��Сʱ��EF��ֵ��С��
����BD��ACʱ����BDΪ�ȱߡ�ABC�ĸ�ʱ��BD��ֵ��С��
��ʱBD= ![]() AC=
AC= ![]() ��
��
���߶�EF����СֵΪ ![]() ��
��
�ߡ�QBA=30�㣬
��ֱ��BQ��y��Ľ���Ϊ��0���� ![]() ����
����
��ֱ��BQ�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ��
��
�ⷽ���� 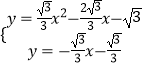 ��
�� ![]() ��
�� ![]() ��
��
���ʱQ�������Ϊ��2���� ![]() ��
��
���������⣺��1����y=0ʱ��x�� ![]() =0�����x=
=0�����x= ![]() ����A��
����A�� ![]() ��0����
��0����
��x=0ʱ��y=x�� ![]() =��
=�� ![]() ����C��0����
����C��0���� ![]() ������B����1��0����C��0����
������B����1��0����C��0���� ![]() ������y=
������y= ![]() x2+bx+c��
x2+bx+c�� 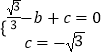 �����
����� 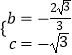 ��
��
���������߽���ʽΪy= ![]() x2��
x2�� ![]() x��
x�� ![]() ��
��
���Դ���y= ![]() x2��
x2�� ![]() x��
x�� ![]() ��
��
�����㾫�����������⣬������Ҫ�˽�һ�κ�����ͼ�������(һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ)����Ҫ���ն��κ�����ͼ��(���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ��)�����֪ʶ���Ǵ���Ĺؼ���

 ��У����ϵ�д�
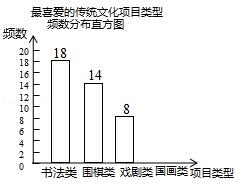
��У����ϵ�д�����Ŀ��ijУΪ���õ�����ѧ����Ȥ����չ����չ�γ��߰�ѡ�Ρ�����������˲���ѧ�����˽�������ϲ������Ŀ���ͣ���Ϊ�鷨��Χ�塢Ϸ�硢������4�ࣩ������ͳ�ƽ�����Ƴ���ͼ��������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�� ��ϲ���Ĵ�ͳ�Ļ���Ŀ����Ƶ���ֲ���
��Ŀ���� | Ƶ�� | Ƶ�� |
�鷨�� | 18 | a |
���� | 14 | 0.28 |
ϲ���� | 8 | 0.16 |
������ | b | 0.20 |
����������Ϣ����������⣺
��1��Ƶ���ֲ�����a= �� b=��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ȫУ����ѧ��1500�������Ƹ�У��ϲ��Χ���ѧ����Լ�ж����ˣ�