题目内容
【题目】如图,△ABC是等边三角形,点D在边AC上(点D不与点A,C重合),点E是射线BC上的一个动点(点E不与点B,C重合),连接DE,以DE为边作等边△DEF,连接CF.
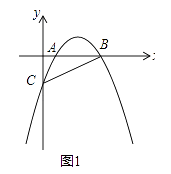
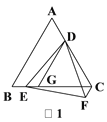
(1)如图1,当DE的延长线与AB的延长线相交,且点C,F在直线DE的同侧时,过点D作DG∥AB,DG交BC于点G,求证:CF=EG;
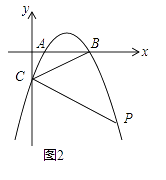
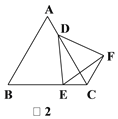
(2)如图2,当DE的反向延长线与AB的反向延长线相交,且点C,F在直线DE的同侧时,求证:CD=CE+CF;
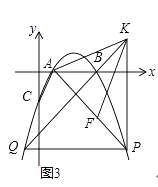
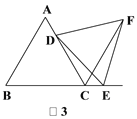
(3)如图3,当DE的反向延长线与线段AB相交,且点C,F在直线DE的异侧时,猜想CD、CE、CF之间的等量关系,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)FC=DC+EC,证明见解析.
【解析】试题分析:(1)根据等边三角形的性质和平行线的性质证出△DCG是等边三角形,得出DC=DG,由△DEF是等边三角形得出DF=DE,然后根据角的关系得出∠EDG=∠FDC,进而得出△EDG≌△FDC,根据全等三角形的性质即可得出结论;
(2)过点D作DG∥AB,DG交BC于点G.同(1)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论;
(3)过点D作DG∥AB,DG交BC于点G.类似于(1)(2)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论.
试题解析:
(1)证明:如图1,∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
∵DG∥AB,
∴∠DGC=∠B.

∴∠DGC=∠DCG=60°.
∴△DGC是等边三角形.
∴DC=DG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°
∴∠EDG=60°-∠GDF,∠FDC=60°-∠GDF,
∴∠EDG=∠FDC,
∴△EDG≌△FDC.
∴FC=EG.
(2)证明:∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
如图2,过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B=60°.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°-∠CDE,∠FDC=60°-∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵CG=CE+EG,
∴CG=CE+FC.
∴CD=CE+FC.
(3)解:如图3,猜想DC、EC、FC之间的等量关系是FC=DC+EC.
证明如下:
∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°.
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°+∠CDE,∠FDC=60°+∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵EG=EC+CG,
∴FC=EC+DC.