��Ŀ����
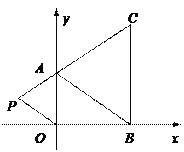
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��B��C���������ֱ�Ϊ(0��a)(b��0)��(b��c)������a��b��c�����ϵʽ(3a��2b)2��![]() ��0��|c��4|��0��
��0��|c��4|��0��
����a��b��c��ֵ��
������ڵڶ���������һ��P(m��1��1)�����ú�m�Ĵ���ʽ��ʾ��AOP�������
���ڢƵ������£�m��ʲô��Χȡֵʱ����AOP����������ڡ�ABC�������������ڷ���������ǰ���¡���AOP��������ʱ��P�����꣮
���𰸡���1����a��2��b��3��c��4�� ��2��S��AOP��1��m����3��P�������Ϊ(��6��1).
����������1���ɷǸ������ʶ����ɵ�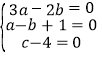 ���ⷽ����ɵ�a,b,c��
���ⷽ����ɵ�a,b,c��
��2����ϵ�A,P,O�����꣬���������������ʽ�ɵõ�S��AOP��1��m��
��3���ֱ���ʽ�ӱ�ʾ���������ε�����������á���AOP����������ڡ�ABC��������͵�P�ڵڶ����ޣ��г�����ʽ�������m��ȡֵ��Χ���ٸ�������ȷ��m=-5ʱ����AOP����������P�����꣮
![]()
��c��4=0��
��a��2��b��3��c��4��
��S��AOP��1��m��
�������ã�B(3��0)��C(3��4)��
��|BC|��4����A��BC�ľ���Ϊ3��
��S��ABC��![]() ��3��4��6��
��3��4��6��
�ߡ�AOP�������������ABC�������S��AOP��1��m��
��S��AOP��S��ABC��S��AOP��1��m��
��1��m��6�����m�ݣ�5����
����P(m��1��1)�ڵڶ������ڣ�
��m��1��0��m��1��
�����١�����֪����5��m��1
����5��m��1ʱ����AOP�������������ABC�������
��S��AOP��1��m����5��m��1
����m����5ʱ����ʱ��AOP��������S��AOP��1��m��6��
��P�������Ϊ(��6��1).

 ��У����ϵ�д�
��У����ϵ�д�