Question

【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A与原点O重合，顶点B在直线l上，将正方形沿射线OB方向无滑动地翻滚．若直线，正方形边长为2

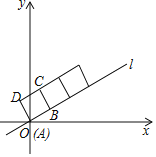
（1）翻滚后点A第一次落在直线l上的坐标是_____；

（2）当正方形翻滚2002次点A对应点的坐标是_____．

Answer 1

【答案】

【解析】

(1)观察图形即可得到翻滚后点A第一次落在直线l上，经过四次翻滚后点A对应一个循环，解直角三角形即可求出点A第一次落在直线l上的坐标.

(2)因为点A四次翻滚为一个循环，所以求出2002除以4的余数和商即可求解.

解：（1）点B在直线上，

∴直线l与x轴夹角为30°，

观察图形，即可得到翻滚后点A第一次落在直线l上，

∴此时OA1＝4×2＝8，

∴此时A1的坐标是（×8，×），

即（12，4）；

（2）观察图形可得经过4次翻滚后点A对应点一循环，

2002÷4＝500…2，

∴经过500次翻滚后点A对应点A2000的坐标为（500×12，500×4），

即（6000，2000），

∴正方形翻滚2002次点A对应点的坐标是（6000+3×，2000+3+3），

即（6009﹣，）

故答案为：（6009﹣，）．