Question

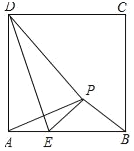
【题目】如图，分别以△ABC的边AB、AC为一边，向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”

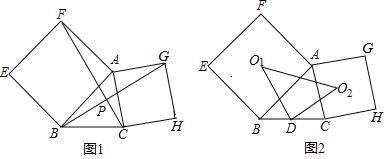
（1）如图1，连接BG，CF相交于点P，求证：BG＝CF且BG⊥CF；

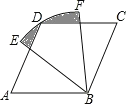
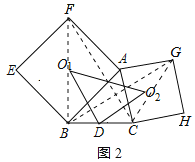
（2）如图2，点D是BC的中点，两个依伴正方形的中心分别为O1，O2连结O1D，O2D，O1O2：，判断△DO1O2的形状并说明由；

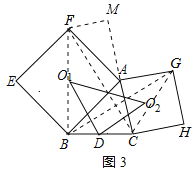
（3）如图2，若AB＝6，AC＝，∠BAC＝60°，求O1O2的长．

Answer 1

【答案】（1）见解析；（2）△DO1O2的形状是等腰直角三角形；理由见解析；（3）

【解析】

(1)由SAS证明△FAC≌△BAG，得出BG＝CF，∠AFC＝∠ABG，设AB与FC的交点为Q,则∠FPG＝∠ABG+∠BQP＝∠AFC+∠AQF＝90°，即可得出结论.

(2)连接FC、BG、FB、GC，证得O1D是△BCF的中位线，得出O1D＝FC，O1D∥FC，同理可得O2D是△CBG的中位线，得出O2D＝BG，O2D∥BG，推出O1D＝O2D，O1D⊥O2D，即可得出结论.

(3)作FM⊥CA交其延长线于点M，证得∠FAM＝180°﹣∠FAB﹣∠BAC＝30°，则MF＝AF＝3，AM＝3，MC＝MA+AC＝6，FC＝，推出O1D＝FC，O1O2＝O1D即可得出结论.

（1）证明：∵四边形ABEF和四边形AGHC是正方形，

∴AF＝AB，AC＝AG，∠FAB＝∠CAG＝90°，

∴∠FAB+∠BAC＝∠CAG+∠BAC，

即∠FAC＝∠BAG，

在△FAC和△BAG中，，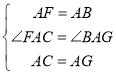

∴△FAC≌△BAG（SAS），

∴BG＝CF，∠AFC＝∠ABG，

∵∠AQF＝∠BQP，

∴∠FPG＝∠ABG+∠BQP＝∠AFC+∠AQF＝90°，

∴BG⊥CF；

（2）解：△DO1O2的形状是等腰直角三角形；理由如下：

连接FC、BG、FB、GC，如图2所示：

由（1）得：FC＝BG，FC⊥BG，

∵O1是正方形ABEF的中心，

∴O1是BF的中点，

∵D是BC的中点，

∴O1D是△BCF的中位线，

∴O1D＝FC，O1D∥FC，

同理O2D是△CBG的中位线，

∴O2D＝BG，O2D∥BG，

∴O1D＝O2D，O1D⊥O2D，

∴△DO1O2为等腰直角三角形；

（3）解：作FM⊥CA交其延长线于点M，如图3所示：

∵四边形ABEF是正方形，

∴AB＝AF＝6，∠FAB＝90°，

∵∠BAC＝60°，

∴∠FAM＝180°﹣∠FAB﹣∠BAC＝30°，

∴MF＝AF＝3，AM＝tan60°FM＝FM＝3，

∴MC＝MA+AC＝6，

∴FC＝，

∴O1D＝FC＝，

∴O1O2＝O1D＝．