题目内容
【题目】四边形ABCD内接于⊙O,AC为对角线,∠ACB=∠ACD
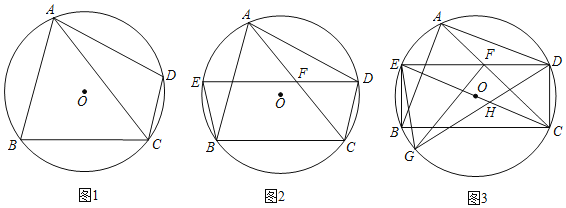
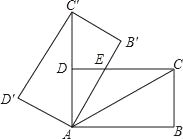
(1)如图1,求证:AB=AD;
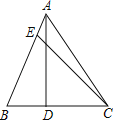
(2)如图2,点E在AB弧上,DE交AC于点F,连接BE,BE=DF,求证:DF=DC;
(3)如图3,在(2)的条件下,点G在BC弧上,连接DG,交CE于点H,连接GE,GF,若DE=BC,EG=GH=5,S△DFG=9,求BC边的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图1,连接OA,OB,OD,由∠ACB=∠ACD,可得![]() ,可得AB=AD;
,可得AB=AD;
(2)连接AE,由“SAS”可证△ABE≌△ADF,可得∠BAE=∠DAC,可证BE=CD=DF;
(3)如图3,过点F作FN⊥GD于N,过点C作CM⊥GD于M,连接GC,通过证明△FDN≌△DCM,可得FN=DM,CM=DN,由面积公式可求FN=2,DM=2,DH=4,通过证明△EGC∽△DMC,△GEH∽△CHD,可得EC=![]() CD,CD2=
CD,CD2=![]() ,由勾股定理可求解.
,由勾股定理可求解.
证明:(1)如图1,连接OA,OB,OD,
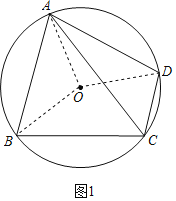
∵∠ACB=∠ACD,∠AOD=2∠ACD,∠AOB=2∠ACB
∴∠AOD=∠AOB
∴![]()
∴AD=AB;
(2)如图2,连接AE,
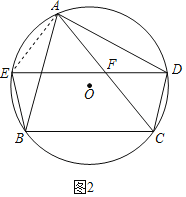
∵![]()
∴∠ABE=∠ADE
在△ABE和△ADF中

∴△ABE≌△ADF(SAS)
∴∠BAE=∠DAC
∴![]()
∴BE=DC
∵BE=DF
∴DF=DC;
(3)如图3,过点F作FN⊥GD于N,过点C作CM⊥GD于M,连接GC,
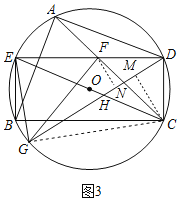
∵DE=BC,BE=CD,
∴四边形BCDE是平行四边形,
∴∠EBC=∠EDC,
∵四边形BEDC是圆内接四边形,
∴∠EBC+∠EDC=180°,
∴∠EDC=∠EBC=90°,
∴EC是直径,
∴∠FGC=∠EDC=90°
∴∠FDN+∠MDC=90°,且∠MDC+∠MCD=90°,
∴∠FDN=∠MCD,且∠FND=∠CMD=90°,DF=DC,
∴△FDN≌△DCM(AAS)
∴FN=DM,CM=DN,
∵EG=GH=5,
∴∠GEH=∠GHE,且∠GHE=∠DHC,∠GEH=∠GDC,
∴∠HDC=∠CHD,
∴CH=CD,且CM⊥DH,
∴DM=MH=FN,
∵S△DFG=9,
∴![]() DG×FN=9,
DG×FN=9,
∴![]() ×(5+2FN)×FN=9,
×(5+2FN)×FN=9,
∴FN=2,
∴DM=2,DH=4,
∵∠GEC=∠GDC,∠EGC=∠DMC,
∴△EGC∽△DMC,
∴![]() ,
,
∴EC=![]() CD,且HC=CD,
CD,且HC=CD,
∴EH=![]() CD,
CD,
∵∠EGD=∠ECD,∠GEC=∠GDC,
∴△GEH∽△CHD,
∴![]() ,
,
∴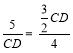 ,
,
∴![]() ,
,
∵EC2﹣CD2=DE2,
∴![]() ,
,
∴![]() ,
,
∴DE=![]()
∴BC=![]()

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某鱼塘中养了某种鱼5000条,为了估计该鱼塘中该种鱼的总质量,从鱼塘中捕捞了3次,取得的数据如下:
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为14元,求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数关系,并估计自变量x的取值范围.