题目内容
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A，B，C，D按顺时针方向排列)，已知AB＝BC＝CD，∠ABC＝100°，∠CAD＝40°，则∠BCD的度数为________．
【答案】80°或100°
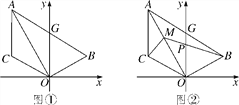
【解析】∵AB＝BC，∠ABC＝100°，∴∠1＝∠2＝∠CAD＝40°，∴AD∥BC.点D的位置有两种情况：(1)如图①，过点C分别作CE⊥AB于E，CF⊥AD于F，∵∠1＝∠CAD，∴CE＝CF，
在Rt△ACE与Rt△ACF中， 
，∴Rt△ACE≌Rt△ACF，∴∠ACE＝∠ACF.
在Rt△BCE与Rt△DCF中， 
，∴Rt△BCE≌Rt△DCF，∴∠BCE＝∠DCF，
∴∠ACD＝∠2＝40°，∴∠BCD＝80°；
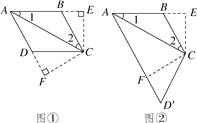
(2)如图②，∵AD′∥BC，AB＝CD′，∴四边形ABCD′是等腰梯形，∴∠BCD′＝∠ABC＝100°，综上所述，∠BCD＝80°或100°，
故答案为：80°或100°.
练习册系列答案
相关题目
