题目内容
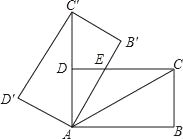
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

【答案】(1)证明见解析;(2)∠BPQ=45°.
【解析】
(1)根据旋转的性质可知,△APD≌△AP′B,所以AP=AP′,∠PAD=∠P′AB,因为∠PAD+∠PAB=90°,所以∠P′AB+∠PAB=90°,即∠PAP′=90°,故△APP′是等腰直角三角形;
(2)根据勾股定理逆定理可判断△PP′B是直角三角形,再根据平角定义求出结果.
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形;
(2)解:∵△APP′是等腰直角三角形,
∴PP′=![]() PA=
PA=![]() ,∠APP′=45°,
,∠APP′=45°,
∵△ADP沿点A旋转至△ABP′,
∴PD=P′B=![]() ,
,
在△PP′B中,PP′=![]() ,PB=2
,PB=2![]() ,P′B=
,P′B=![]() ,
,
∵(![]() )2+(2
)2+(2![]() )2=(
)2=(![]() )2,
)2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°﹣∠APP′﹣∠P′PB=180°﹣45°﹣90°=45°.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目