ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() ÓėxÖį½»ÓŚµćC£¬ÓėyÖį½»ÓŚµćB£¬Å×ĪļĻß
ÓėxÖį½»ÓŚµćC£¬ÓėyÖį½»ÓŚµćB£¬Å×ĪļĻß![]() ¾¹żB”¢CĮ½µć£®
¾¹żB”¢CĮ½µć£®
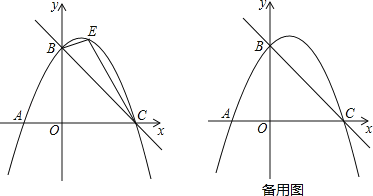
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
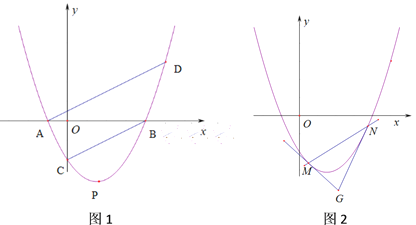
£Ø2£©ČēĶ¼£¬µćEŹĒÅ×ĪļĻßÉĻµÄŅ»¶Æµć£Ø²»ÓėB£¬CĮ½µćÖŲŗĻ£©£¬”÷BECĆ껿¼ĒĪŖS£¬SČ”ŗĪÖµŹ±£¬¶ŌÓ¦µÄµćEÓŠĒŅÖ»ÓŠĮ½øö£æ
£Ø3£©Ö±Ļßx=2½»Ö±ĻßBCÓŚµćM£¬µćQŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄ¶Æµć£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌP”¢Q”¢A”¢MĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y£½©![]() x2+
x2+![]() x+3£»£Ø2£©µ±S>3Ź±¶ŌÓ¦µÄEµćÓŠĒŅÖ»ÓŠ2øö.£Ø3£©“ęŌŚ£¬µćPµÄ×ų±źŹĒ£Ø©3£¬©
x+3£»£Ø2£©µ±S>3Ź±¶ŌÓ¦µÄEµćÓŠĒŅÖ»ÓŠ2øö.£Ø3£©“ęŌŚ£¬µćPµÄ×ų±źŹĒ£Ø©3£¬©![]() £©£¬£Ø5£¬©
£©£¬£Ø5£¬©![]() £©£¬£Ø©1£¬
£©£¬£Ø©1£¬![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©ĻČĒó³öµćB”¢CµÄ×ų±ź£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·Ø£¬¼“æÉĒó³ö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©¹żµćE×÷yÖįµÄĘ½ŠŠĻßEF½»Ö±ĻßBCÓŚµćM£¬EF½»xÖįÓŚµćF£¬µ±µćEŌŚBCÉĻ·½ŌĖ¶ÆŹ±£¬Ēó³ö”÷BECµÄĆ껿µÄ×ī“óÖµ£¬“ĖŹ±“ęŌŚ3øöµć£»µ±Ć껿“óÓŚ3Ź±£¬µćEÖ»ÄÜŌŚBCµÄĻĀ·½ŌĖ¶Æ£¬¶ŌÓ¦µÄµćEÓŠĒŅÖ»ÓŠĮ½øö£¬¼“æɽā“š£»
£Ø3£©øł¾ŻĢāŅā£¬ĻČĒó³öµćAŗĶµćMµÄ×ų±ź£¬ŅŌ¼°µćQµÄŗį×ų±ź£¬Č»ŗóøł¾ŻĘ½ŠŠĖıߊĪµÄÅŠ¶ØŗĶŠŌÖŹ½ųŠŠ½ā“š£»æÉ·ÖĪŖČżÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ¢Łµ±AMĪŖ¶Ō½ĒĻߏ±£»¢Śµ±AQŹĒ¶Ō½ĒĻߏ±£»¢Ūµ±MQŹĒ¶Ō½ĒĻߏ±£»¼“æɽā¾öĪŹĢā.
½ā£ŗ£Ø1£©”ßÖ±Ļßy£½©![]() x+3ÓėxÖį½»ÓŚµćC£¬ÓėyÖį½»ÓŚµćB£¬
x+3ÓėxÖį½»ÓŚµćC£¬ÓėyÖį½»ÓŚµćB£¬
”ąµćBµÄ×ų±źŹĒ£Ø0£¬3£©£¬µćCµÄ×ų±źŹĒ£Ø4£¬0£©£¬
”ßÅ×ĪļĻßy£½ax2+![]() x+c¾¹żB”¢CĮ½µć£¬
x+c¾¹żB”¢CĮ½µć£¬
”ą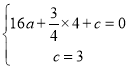 £¬
£¬
½āµĆ£ŗ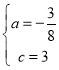 £¬
£¬
”ą![]() £»
£»
£Ø2£©ČēĶ¼1£¬µ±µćEŌŚÖ±ĻßBCÉĻ·½Å×ĪļĻßÉĻµÄŅ»¶ÆµćŹ±£¬¹żµćE×÷yÖįµÄĘ½ŠŠĻßEF½»Ö±ĻßBCÓŚµćM£¬EF½»xÖįÓŚµćF.
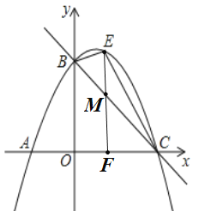
µ±µćEŌŚÖ±ĻßBCÉĻ·½Å×ĪļĻßÉĻµÄŅ»¶ÆµćŹ±£¬
ÉčµćEµÄ×ų±źŹĒ£Øx£¬![]() £©£¬
£©£¬
ŌņµćMµÄ×ų±źŹĒ£Øx£¬![]() £©£¬
£©£¬
”ąEM£½![]() ©£Ø
©£Ø![]() £©£½
£©£½![]() £¬
£¬
”ąS”÷BEC£½S”÷BEM+S”÷MEC
![]()
£½![]()
£½![]()
£½![]()
£½![]() £»
£»
”ß![]() £¬
£¬
”ąµ±x£½2Ź±£¬¼“µćEµÄ×ų±źŹĒ£Ø2£¬3£©Ź±£¬”÷BECµÄĆ껿×ī“ó£¬×ī“óĆ껿ŹĒ3£®
”ąµ±S>3Ź±¶ŌÓ¦µÄEµćÓŠĒŅÖ»ÓŠ2øö£»
£Ø3£©øł¾ŻĢāŅā£¬Å×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ![]() £¬
£¬
”ąÅ×ĪļĻߵĶŌ³ĘÖįĪŖ£ŗ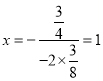 £¬
£¬
”ąµćQµÄŗį×ų±źĪŖ1£»
µ±![]() Ź±£¬“śČėÖ±Ļß·½³Ģ£¬µĆ£ŗ
Ź±£¬“śČėÖ±Ļß·½³Ģ£¬µĆ£ŗ![]() £¬
£¬
”ąµćM×ų±źĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£¬
£©£¬
Įī![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() »ņ
»ņ![]() £¬
£¬
”ąµćAĪŖ![]() £¬µćCĪŖ£Ø4£¬0£©£»
£¬µćCĪŖ£Ø4£¬0£©£»
”ßÓÉŅŌP”¢Q”¢A”¢MĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ÓŠŅŌĻĀĒéæö£ŗ
¢Łµ±AMĪŖ¶Ō½ĒĻߏ±£¬ČēĶ¼£ŗ
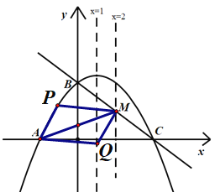
“ĖŹ±AMÖŠµćµÄŗį×ų±źĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£¬
£©£¬
”ßµćQµÄŗį×ų±źĪŖ1£¬ŌņµćPµÄŗį×ų±źĪŖ![]() £¬
£¬
°Ń![]() “śČėÅ×ĪļĻßµĆ£ŗ
“śČėÅ×ĪļĻßµĆ£ŗ![]() £¬
£¬
”ąµćP×ų±źĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£»
£©£»
¢Śµ±AQŹĒ¶Ō½ĒĻߏ±£¬ČēĶ¼£ŗ
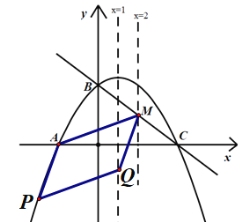
“ĖŹ±AQÖŠµćµÄŗį×ų±źĪŖ£ŗ![]() £¬
£¬
”ßµćMµÄŗį×ų±źĪŖ2£¬ŌņµćPµÄŗį×ų±źĪŖ![]() £»
£»
°Ń![]() “śČėÅ×ĪļĻßµĆ£ŗ
“śČėÅ×ĪļĻßµĆ£ŗ![]() £¬
£¬
”ąµćPĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£»
£©£»
¢Ūµ±MQŹĒ¶Ō½ĒĻߏ±£¬ČēĶ¼£ŗ
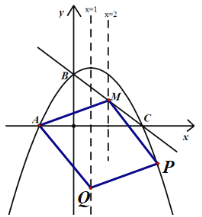
“ĖŹ±MQÖŠµćµÄŗį×ų±źĪŖ£ŗ![]() £¬
£¬
”ßµćAµÄŗį×ų±źĪŖ![]() £¬ŌņµćPµÄŗį×ų±źĪŖ5£»
£¬ŌņµćPµÄŗį×ų±źĪŖ5£»
°Ń![]() “śČėÅ×ĪļĻß½āĪöŹ½µĆ£ŗ
“śČėÅ×ĪļĻß½āĪöŹ½µĆ£ŗ![]() £¬
£¬
”ąµćPĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£»
£©£»
×ŪŗĻÉĻŹö£¬µćPµÄ×ų±źŹĒ£ŗ£Ø©1£¬![]() £©»ņ£Ø©3£¬
£©»ņ£Ø©3£¬![]() £©»ņ£Ø5£¬
£©»ņ£Ø5£¬![]() £©£®
£©£®