题目内容
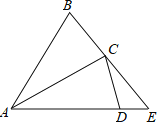
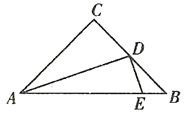
【题目】如图，在
中，
，
，点
为腰
中点，点
在底边
上，且
，则
的长为______.
【答案】
【解析】
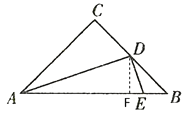
过点D作DF⊥AB于F，根据等腰三角形的性质和已知条件可得：
，∠B=45°，根据勾股定理求出AD和AB，根据等腰直角三角形的判定即可证出：△DFB是等腰直角三角形和BF的长，然后根据相似三角形的判定可得：△ADE∽△AFD，根据相似三角形的性质列出比例式，即可求出AE，从而求出BE.
解：过点D作DF⊥AB于F
∵
，
，点
为腰
中点，
∴，∠B=45°
根据勾股定理可得：AD=
，AB=
∵
，DF⊥AB
∴△DFB是等腰直角三角形，BF=
，∠ADE=∠AFD
∴AF=AB－BF=
∵∠DAE=∠FAD
∴△ADE∽△AFD
∴
即：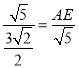
解得：
∴
故答案为: .
练习册系列答案
阅读快车系列答案
相关题目
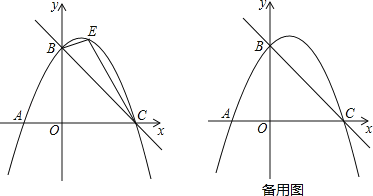
【题目】某数学兴趣小组根据学习函数的经验，对分段函数y＝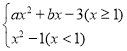
的图象与性质进了探究，请补充完整以下的探索过程．
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | ﹣1 | 0 | 1 | 0 | ﹣3 | … |
（1）填空：a＝ ．b＝ ．
（2）①提上述表格补全函数图象；②该函数图象是关于 对称的 （横线上填轴对称或中心对称）图形．
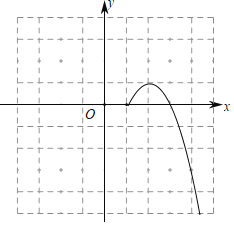
（3）若直线y＝
x+t与该函数图象有三个交点，直接写出t的取值范围．
