题目内容
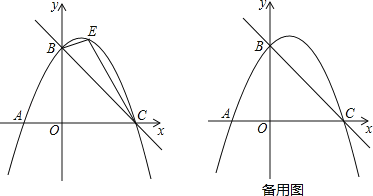
【题目】已知抛物线
与
轴交于A，B两点(A在B左边)，与
轴交于C点，顶点为P，OC=2AO.
(1)求
与
满足的关系式；
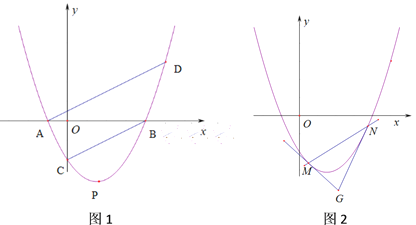
(2)直线AD//BC，与抛物线交于另一点D，△ADP的面积为
，求的值；
(3)在(2)的条件下，过(1，-1)的直线与抛物线交于M、N两点，分别过M、N且与抛物线仅有一个公共点的两条直线交于点G，求OG长的最小值.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）将抛物线解析式进行因式分解，可求出A点坐标，得到OA长度，再由C点坐标得到OC长度，然后利用OC=2AO建立等量关系即可得到关系式；
（2）利用待定系数法求出直线BC的k，根据平行可知AD直线的斜率k与BC相等，可求出直线AD解析式，与抛物线联立可求D点坐标，过P作PE⊥x轴交AD于点E，求出PE即可表示△ADP的面积，从而建立方程求解；
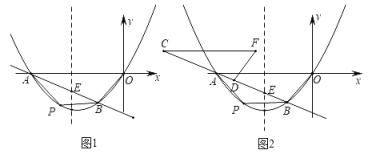
（3）为方便书写，可设抛物线解析式为：
，设
，
，过点M的切线解析式为
，两抛物线与切线联立，由
可求k，得到M、N的坐标满足
，将（1，-1）代入，推出G为直线
上的一点，由垂线段最短，求出OG垂直于直线时的值即为最小值.
解：（1）
令y=0，
，解得
，
令x=0，则
∵
， A在B左边
∴A点坐标为（-m，0），B点坐标为（4m，0），C点坐标为（0，-4am2）
∴AO=m，OC=4am2
∵OC=2AO
∴4am2=2m
∴
（2）∵
∴C点坐标为（0，-2m）
设BC直线为
，代入B（4m，0），C（0，-2m）得
，解得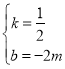
∵AD∥BC，
∴设直线AD为
，代入A（-m，0）得，
，
∴
∴直线AD为
直线AD与抛物线联立得，
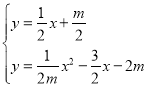，解得
或
∴D点坐标为（5m，3m）
又∵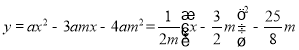
∴顶点P坐标为
如图，过P作PE⊥x轴交AD于点E，则E点横坐标为
，代入直线AD得
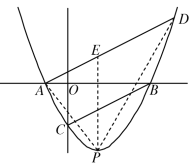
∴PE=
∴S△ADP=
解得
∵m＞0
∴
∴
.
（3）在（2）的条件下，可设抛物线解析式为：，
设，，过点M的切线解析式为，
将抛物线与切线解析式联立得：
，整理得
，
∵
，
∴方程可整理为
∵只有一个交点，
∴
整理得
即
解得
∴过M的切线为
同理可得过N的切线为
由此可知M、N的坐标满足
将
代入整理得
将（1，-1）代入得
在（2）的条件下，抛物线解析式为
，即
∴
整理得
∴G点坐标满足，即G为直线上的一点，
当OG垂直于直线时，OG最小，如图所示，
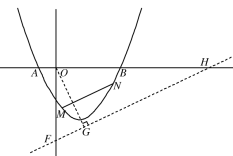
直线与x轴交点H（5,0），与y轴交点F（0，
）
∴OH=5，OF=
，FH=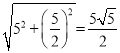
∵
∴
∴OG的最小值为.
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
