��Ŀ����
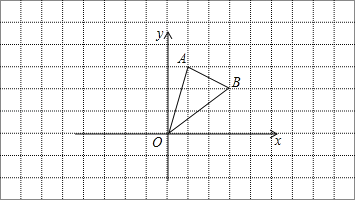
����Ŀ����ͼ����֪Rt��ABC�У���C��90����AC��6��BC��8����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�B��A�����˶���Q����A���P��Ҳֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
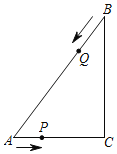
��1����P��ֹͣ�˶�ʱ��BP�ij���
��2��P��Q�������˶������У���E��Q�����ֱ��AC�ĶԳƵ㣬�Ƿ����ʱ��t��ʹ�ı���PQCEΪ���Σ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��3��P��Q�������˶������У���ʹ��APQ����ABC���Ƶ�ʱ��t��ֵ��
���𰸡���1��![]() ����2�����ڣ�t��
����2�����ڣ�t��![]() sʱ���ı���PQCE�����Σ���3��t��ֵΪ
sʱ���ı���PQCE�����Σ���3��t��ֵΪ![]() s��
s��![]() sʱ��APQ����ABC����
sʱ��APQ����ABC����
��������
��1�������Q�Ĵ�B��A���˶�ʱ�䣬�����AP�ij������ù��ɶ������ɽ�����⣮
��2����ͼ1�У����ı���PQCE������ʱ������QE��AC��K����QD��BC��D������DQ��CK���������̼��ɽ�����⣮
��3�����������Σ���ͼ3��1�У�����APQ��90��ʱ����ͼ3��2�У�����AQP��90��ʱ���ֱ����̼��ɽ�����⣮
�⣺��1����Rt��ABC�У��ߡ�C��90����AC��6��BC��8��
��AB��![]() ��10��
��10��
��Q�˶�����Aʱ��t��![]() ��5��
��5��
��AP��5��PC��1��
��Rt��PBC��PB��![]() ��
��![]() ��
��
��2����ͼ1�У����ı���PQCE������ʱ������QE��AC��K����QD��BC��D��
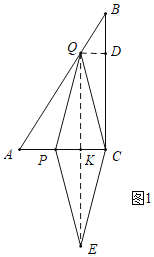
���ı���PQCE�����Σ�
��PC��EQ��PK��KC��
�ߡ�QKC����QDC����DCK��90����
���ı���QDCK�Ǿ��Σ�
��DQ��CK��
��![]() 2t��
2t��![]() ��6��t����
��6��t����
���t��![]() ��
��
��t��![]() sʱ���ı���PQCE�����Σ�
sʱ���ı���PQCE�����Σ�
��3����ͼ3��1�У�����APQ��90��ʱ��
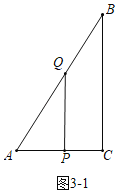
�ߡ�APQ����C��90����
��PQ��BC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��t��![]() ��
��
��ͼ3��2�У�����AQP��90��ʱ��
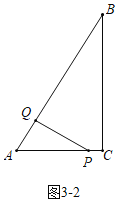
�ߡ�AQP�ס�ACB��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��t��![]() ��
��
����������t��ֵΪ![]() s��
s��![]() sʱ��APQ����ABC���ƣ�
sʱ��APQ����ABC���ƣ�

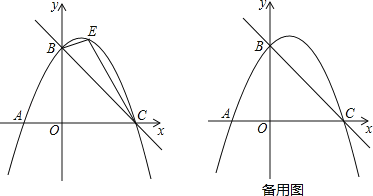
����Ŀ��������y��ax2+bx+c��a��0��a��b��cΪ�������ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | ���� | ��3 | ��2 | ��1 | 0 | 1 | 2 | ���� |
y | ���� |
| 4 |
| 4 | m | 0 | ���� |
�����н����У��������ߵĶԳ���Ϊֱ��x����1����m��![]() ���۵���4��x��2ʱ��y��0���ܷ���ax2+bx+c��4��0�������ֱ���x1����2��x2��0��������ȷ�ĸ����У�������
���۵���4��x��2ʱ��y��0���ܷ���ax2+bx+c��4��0�������ֱ���x1����2��x2��0��������ȷ�ĸ����У�������
A.1��B.2��C.3��D.4��