МвДїДЪИЭ
ЎѕМвДїЎїРЎАоµД»оУгЕъ·ўµкТФ 44 ФЄ/№«ЅпµДјЫёсґУёЫїЪВтЅшТ»Еъ 2000 №«ЅпµДДіЖ·ЦЦ»оУгЈ¬ФЪФЛКд№эіМЦРЈ¬УРІї·ЦУгОґДЬґж»оЈ¬РЎАо¶ФФЛµЅµДУгЅшРРЛж»ъійІйЈ¬Ѕб№ыИз±нТ».УЙУЪ КРіЎµчЅЪЈ¬ёГЖ·ЦЦ»оУгµДКЫјЫУлИХПъКЫБїЦ®јдУРТ»¶ЁµД±д»Ї№жВЙЈ¬±н¶юКЗЅьТ»¶ОК±јдёГЕъ·ўµкµДПъКЫјЗВј.
±нТ»
ЛщійІйµДУгµДЧЬЦШБї m(№«Ѕп) | 100 | 150 | 200 | 250 | 350 | 450 | 500 |
ґж»оµДУгµДЦШБїУл m µД±ИЦµ | 0.885 | 0.876 | 0.874 | 0.878 | 0.871 | 0.880 | 0.880 |
±н¶ю
ёГЖ·ЦЦ»оУгµДКЫјЫ(ФЄ/№«Ѕп) | 50 | 51 | 52 | 53 | 54 |
ёГЖ·Йс»оУгµДИХПъКЫБї(№«Ѕп) | 400 | 360 | 320 | 280 | 240 |
(1)Зл№АјЖФЛµЅµД 2000 №«ЅпУгЦР»оУгµДЧЬЦШБїЈ»(Ц±ЅУРґіцґр°ё)
(2)°ґґЛКРіЎµчЅЪµД№ЫВЙЈ¬
ўЩИфёГЖ·ЦЦ»оУгµДКЫјЫ¶ЁОЄ 52.5 ФЄ/№«ЅпЈ¬Зл№АјЖИХПъКЫБїЈ¬ІўЛµГчАнУЙЈ»
ўЪїјВЗµЅёГЕъ·ўµкµДґўґжМхЈ¬РЎАоґтЛг 8 МмДЪВфНкХвЕъУг(Ц»Вф»оУг)Ј¬ЗТКЫјЫ±ЈіЦ І»±дЈ¬ЗуёГЕъ·ўµкГїИХВфУгїЙДЬґпµЅµДЧоґуАыИуЈ¬ІўЛµГчАнУЙ.
Ўѕґр°ёЎїЈЁ1Ј©1760№«ЅпЈ»ЈЁ2Ј©ўЩ300№«ЅпЈ¬АнУЙјыЅвОцўЪ990ФЄЈ¬АнУЙјыЅвОц.
ЎѕЅвОцЎї
ЈЁ1Ј©УЙ±нТ»їЙЦЄЈ¬ёГЖ·ЦЦ»оУгµДґж»оВКФјОЄ0.88Ј¬ФтУГ2000іЛТФ0.88јґїЙµГЈ»
ЈЁ2Ј©ўЩУЙ±н¶юїЙЦЄЈ¬КЫјЫГїФцјУ1ФЄЈ¬ИХПъКЫБїѕН»бјхЙЩ40№«ЅпЈ¬УЙґЛјґїЙЗуЅвЈ»
ўЪПИёщѕЭёГЖ·ЦЦ»оУгµДКЫјЫУлИХПъКЫБїЦ®јдµД±д»Ї№жВЙЈ¬ЗуіцЖд±д»ЇµД№ШПµКЅЈ»ФЩёщѕЭЎ°АыИуЈЅГї№«ЅпАыИуЎБПъКЫБїЎ±БРіцєЇКэЅвОцКЅЈ¬ІўЅбєПМвЦРµДёш¶ЁµДМхјюЈ¬µГіцЧФ±дБїµДИЎЦµ·¶О§Ј¬АыУГ¶юґОєЇКэµДРФЦКЗуЅвјґїЙ.
ЈЁ1Ј©УЙ±нТ»їЙЦЄЈ¬ёГЖ·ЦЦ»оУгµДґж»оВКФјОЄ0.88Ј¬
Фт№АјЖФЛµЅµД 2000 №«ЅпУгЦР»оУгµДЧЬЦШБїОЄЈє![]() ЈЁ№«ЅпЈ©Ј»
ЈЁ№«ЅпЈ©Ј»
ЈЁ2Ј©ўЩУЙ±н¶юїЙЦЄЈ¬КЫјЫГїФцјУ1ФЄЈ¬ИХПъКЫБїѕН»бјхЙЩ40№«ЅпЈ¬
ФтЛщЗуµД№АјЖИХПъКЫБїОЄЈє![]() ЈЁ№«ЅпЈ©Ј»
ЈЁ№«ЅпЈ©Ј»
ўЪЙиХв8МмёГ»оУгµДКЫјЫОЄ![]() ФЄ/№«ЅпЈ¬¶ФУ¦µДИХПъКЫБїОЄ
ФЄ/№«ЅпЈ¬¶ФУ¦µДИХПъКЫБїОЄ![]() №«ЅпЈ¬ёщѕЭёГЖ·ЦЦ»оУгµДКЫјЫУлИХПъКЫБїЦ®јдµД±д»Ї№жВЙїЙЦЄЈ¬
№«ЅпЈ¬ёщѕЭёГЖ·ЦЦ»оУгµДКЫјЫУлИХПъКЫБїЦ®јдµД±д»Ї№жВЙїЙЦЄЈ¬![]() Ул
Ул![]() Ц®јдґжФЪПЯРФ№ШПµЈ¬ФтЙи
Ц®јдґжФЪПЯРФ№ШПµЈ¬ФтЙи![]()
УЙ±н¶юµГЈєµ±![]() К±Ј¬
К±Ј¬![]() Ј»µ±
Ј»µ±![]() К±Ј¬
К±Ј¬![]() Ј¬
Ј¬
ґъИлµГЈє![]() Ј¬ЅвµГЈє
Ј¬ЅвµГЈє![]() Ј¬
Ј¬
Фт![]() Ј¬
Ј¬
ЙиёГЕъ·ўµкГїИХВфУгµДАыИуОЄ![]() Ј¬
Ј¬
УЙМвТвµГЈє![]() Ј¬
Ј¬
јґ![]() Ј¬
Ј¬
УЦТтТЄФЪ8МмДЪВфНкХвЕъУгЈ¬Фт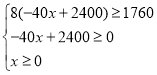 Ј¬
Ј¬
ЅвµГЈє![]() Ј¬
Ј¬
УЙ¶юґОєЇКэµДРФЦКїЙЦЄЈ¬ЕЧОпПЯ![]() µДїЄїЪПтПВЈ¬µ±
µДїЄїЪПтПВЈ¬µ±![]() К±Ј¬
К±Ј¬![]() Лж
Лж![]() µДФцґу¶шФцґуЈ¬
µДФцґу¶шФцґуЈ¬
№Кµ±![]() К±Ј¬
К±Ј¬![]() ИЎµГЧоґуЦµЈ¬ЧоґуЦµОЄ
ИЎµГЧоґуЦµЈ¬ЧоґуЦµОЄ![]() ФЄЈ¬
ФЄЈ¬
ґрЈєЛщЗуёГЕъ·ўµкГїИХВфУгїЙДЬґпµЅµДЧоґуАыИуОЄ990ФЄ.