题目内容
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
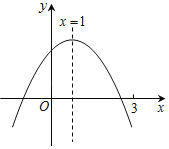
A.①②③B.②④C.②⑤D.②③⑤
【答案】C
【解析】
由抛物线的开口方向、抛物线的对称轴及抛物线与![]() 轴的交点判断①②,由顶点坐标确定函数最大值是a+b+c判断③,然后根据抛物线与
轴的交点判断①②,由顶点坐标确定函数最大值是a+b+c判断③,然后根据抛物线与![]() 轴交点的个数及对称轴判断④,由ax12+bx1=ax22+bx2恒等变形得x1+x2=
轴交点的个数及对称轴判断④,由ax12+bx1=ax22+bx2恒等变形得x1+x2=![]() ,根据对称轴直线x=
,根据对称轴直线x=![]() =1,可以判断⑤.
=1,可以判断⑤.
∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=![]() =1,
=1,
∴b=﹣2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③错误;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=![]() ,
,
∵b=﹣2a,
∴x1+x2=2,所以⑤正确.
综上所述,正确的有②⑤.
故选:C.

【题目】小李的活鱼批发店以 44 元/公斤的价格从港口买进一批 2000 公斤的某品种活鱼,在运输过程中,有部分鱼未能存活,小李对运到的鱼进行随机抽查,结果如表一.由于 市场调节,该品种活鱼的售价与日销售量之间有一定的变化规律,表二是近一段时间该批发店的销售记录.
表一
所抽查的鱼的总重量 m(公斤) | 100 | 150 | 200 | 250 | 350 | 450 | 500 |
存活的鱼的重量与 m 的比值 | 0.885 | 0.876 | 0.874 | 0.878 | 0.871 | 0.880 | 0.880 |
表二
该品种活鱼的售价(元/公斤) | 50 | 51 | 52 | 53 | 54 |
该品神活鱼的日销售量(公斤) | 400 | 360 | 320 | 280 | 240 |
(1)请估计运到的 2000 公斤鱼中活鱼的总重量;(直接写出答案)
(2)按此市场调节的观律,
①若该品种活鱼的售价定为 52.5 元/公斤,请估计日销售量,并说明理由;
②考虑到该批发店的储存条,小李打算 8 天内卖完这批鱼(只卖活鱼),且售价保持 不变,求该批发店每日卖鱼可能达到的最大利润,并说明理由.