Question

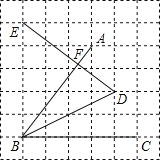
【题目】如图是由边长为1的小正方形组成的网格图，线段AB，BC，BD，DE的端点均在格点上，线段AB和DE交于点F，则DF的长度为_____．

Answer 1

【答案】2

【解析】

连接AD、CD，由勾股定理得：，，，得出AB＝DE＝BC，，由此可得△ABD为直角三角形，同理可得△BCD为直角三角用形，继而得出A、D、C三点共线.再证明△ABC≌△DEB，得出∠BAC＝∠EDB，得出DF⊥AB，BD平分∠ABC，再由角平分线的性得出DF＝DG＝2即可的解.

连接AD、CD，如图所示：

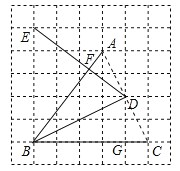
由勾股定理可得，

，，，

∵BE=BC=5，∴AB=DE＝AB＝BC ，，

∴△ABD是直角三角形，∠ADB＝90°，

同理可得：△BCD是直角三角形，∠BDC＝90°，

∴∠ADC＝180°，∴点A、D、C三点共线，

∴，

在△ABC和△DEB中，

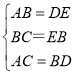，∴△ABC≌△DEB(SSS)，∴∠BAC＝∠EDB，

∵∠EDB+∠ADF＝90°，∴∠BAD+∠ADF＝90°，

∴∠BFD＝90°，∴DF⊥AB，

∵AB=BC，BD⊥AC，∴BD平分∠ABC，

∵DG⊥BC，∴DF＝DG＝2.