Question

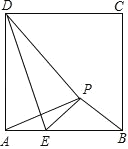
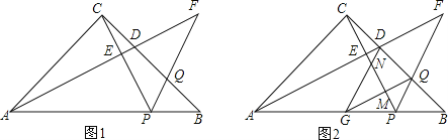
【题目】 如图，在Rt△ABC中，∠ACB=90°，AC=BC．点P为AB边上一点，Q为BC边上一点，且∠BPQ=∠APC，过点A作AD⊥PC，交BC于点D，直线AD分别交直线PC、PQ于E、F．

（1）求证：∠FDQ=∠FQD；

（2）把△DFQ沿DQ边翻折，点F刚好落在AB边上点G，设PC分别交GQ、GD于M、N，试判定MN与EN的数量关系，并给予证明．

Answer 1

【答案】（1）详见解析；（2）MN=3EN，证明详见解析

【解析】

（1）首先根据∠ACB=90°，AC=BC，可得∠BAC=∠ABC=45°；然后根据三角形的外角的性质，可得∠FDQ=∠FAB+∠ABC=∠FAB+45°；最后在△BPQ中，根据三角形的内角和定理，推得∠FQD=∠BQP=∠FAB+45°，即可推得∠FDQ=∠FQD．

（2）MN与EN的数量关系是：MN=3EN．首先判断出AH∥DG∥PQ，推得，再根据相似三角形判定的方法，判断出△APC∽△BPQ，推得，进一步推得BQ=HC=CD；然后判断出AH∥PF，推得=，进一步推得DQ=CD，BP=PG，再根据BI∥GQ，推得BI=GM；最后判断出AD∥BI，即可推得，据此判断出MN=3EN即可．

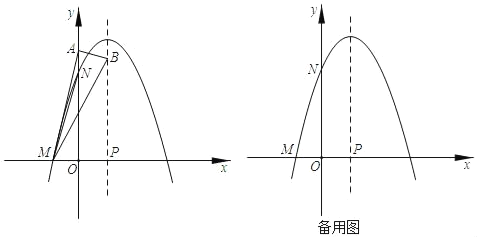
（1）证明：如图1，

，

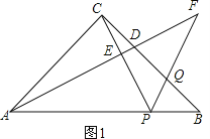∵∠ACB=90°，AC=BC，

∴∠BAC=∠ABC=45°，

由三角形的外角的性质，可得

∠FDQ=∠FAB+∠ABC=∠FAB+45°，

∵AD⊥PC，

∴∠AEP=90°，

∴∠FAB+∠APC=90°，

∴∠APC=90°-∠FAB，

又∵∠BPQ=∠APC，

∴∠BPQ=90°-∠FAB，

∴∠FQD=∠BQP=180°-∠BPQ-∠ABC

=180°-（90°-∠FAB）-45°

=∠FAB+45°

∴∠FDQ=∠FQD．

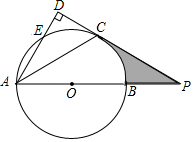
（2）解：MN与EN的数量关系是：MN=3EN．

如图2，延长DC至H，使HC=CD，连接AH，过点B作BI∥GQ，交CP延长线于点I，

，

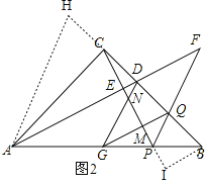∵HC=CD，AC⊥HD，

∴△ADH是等腰三角形，

∴AD=AH，

∴∠H=∠ADH=∠FDQ=∠FQD=∠BQP，

∵把△DFQ沿DQ边翻折，得到△DGQ，

∴△GDQ≌△FDQ，

∴∠FDQ=∠GDQ，

又∵∠H=∠FDQ=∠BQP，

∴∠H=∠BQP=∠GDQ，

∴AH∥DG∥PQ，

∴，∠GQP=∠DGQ，

在△APC和△BPQ中，

，

∴△APC∽△BPQ，

∴，

又∵，

∴，

∴BC=QH，

∴BQ=HC，

又∵HC=CD，

∴BQ=HC=CD．

∵把△DFQ沿DQ边翻折，得到△DGQ，

∴∠DFQ=∠DGQ，

又∵∠GQP=∠DGQ，

∴∠GQP=∠DFQ，

∴AD∥GQ，四边形DFQG是平行四边形，

∴，FD=GQ，

∵AH∥PF，

∴=，

又∵DH=2CD，BQ=CD，

∴，

∴，

∴（DQ+2CD）（DQ-CD）=0，

解得DQ=CD，或DQ=-2CD（舍去），

∵=1，

∴BP=PG，

∵BI∥GQ，

∴=1，

∴BI=GM，

∵BI∥GQ，AD∥GQ，

∴AD∥BI，

∴，

∴，

∴，

∴MN=3EN．