Question

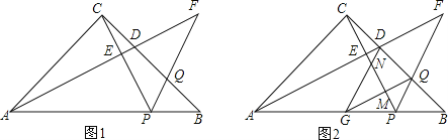
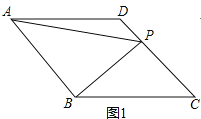
【题目】菱形ABCD中，点P为CD上一点，连接BP．

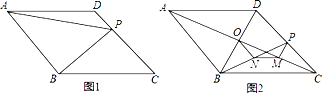
（1）如图1，若BP⊥CD，菱形ABCD边长为10，PD＝4，连接AP，求AP的长．

（2）如图2，连接对角线AC、BD相交于点O，点N为BP的中点，过P作PM⊥AC于M，连接ON、MN．试判断△MON的形状，并说明理由．

Answer 1

【答案】（1）2；（2）△OMN是等腰三角形，理由见解析

【解析】

（1）在Rt△BCP中利用勾股定理求出PB，在Rt△ABP中利用勾股定理求出PA即可．

（2）如图2中，延长PM交BC于E．先证明PD=BE，再利用三角形中位线定理证明MN=BE，ON=PD即可．

（1）如图1中，∵四边形ABCD是菱形，

∴AB＝BC＝CD＝AD＝10，AB∥CD

∵PD＝4，

∴PC＝6，

∵PB⊥CD，

∴PB⊥AB，

∴∠CPB＝∠ABP＝90°，

在Rt△PCB中，∵∠CPB＝90°，PC＝6，BC＝10，

∴PB＝＝8，

在Rt△ABP中，∵∠ABP＝90°，AB＝10，PB＝8，

∴PA＝＝＝2．

（2）△OMN是等腰三角形．

理由：如图2中，延长PM交BC于E．

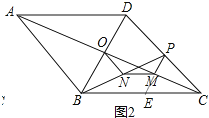
∵四边形ABCD是菱形，

∴AC⊥BD，CB＝CD，

∵PE⊥AC，

∴PE∥BD，

∴＝，

∴CP＝CE，

∴PD＝BE，

∵CP＝CE，CM⊥PE，

∴PM＝ME，

∵PN＝NB，

∴MN＝BE，

∵BO＝OD，BN＝NP，

∴ON＝PD，

∴ON＝MN，

∴△OMN是等腰三角形．