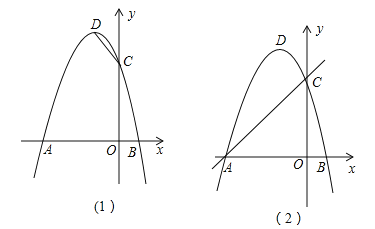题目内容
【题目】如图,抛物线 ![]() 与X轴交于点(―3,0),其对称轴为直线
与X轴交于点(―3,0),其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ; ②
; ②![]() ;③当
;③当![]() 时,y 随x 的增大而增大,④一元二次方程
时,y 随x 的增大而增大,④一元二次方程![]() 的两根分别为
的两根分别为![]() ;⑤若
;⑤若![]() (
(![]() )为方程
)为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
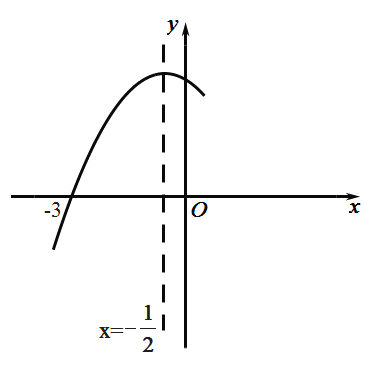
A.3个B.4个C.5个D.6个
【答案】A
【解析】
根据抛物线开口向下和对称轴的位置,抛物线与y轴交于正半轴,可得:a<0,b<0,c>0,即可判断①;由9a-3b+c=0,结合:b=a,a<0,即可判断②;根据抛物线开口向下,对称轴为直线![]() ,即可判断③;由
,即可判断③;由![]() 的两根是:
的两根是:![]() ,得:
,得:![]() 的两根是:
的两根是:![]() ,进而得:
,进而得:![]() 的两根,即可判断④;由
的两根,即可判断④;由![]() (
(![]() )为方程
)为方程![]() 的两个根,得:
的两个根,得:![]() (
(![]() )为抛物线
)为抛物线![]() =
=![]() 和直线y=-3的两个交点的横坐标,结合图象,即可得到m,n的范围,即可判断⑤.
和直线y=-3的两个交点的横坐标,结合图象,即可得到m,n的范围,即可判断⑤.
∵抛物线开口向下,
∴a<0,
∵对称轴为:直线![]() ,
,
∴![]() ,即:b=a,
,即:b=a,
∴b<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴![]() ,
,
故①正确;
∵抛物线 ![]() 与x轴交于点(-3,0),
与x轴交于点(-3,0),
∴9a-3b+c=0,
∵a=b,
∴c=-6a,
∴3a+c=-3a>0,
故②正确;
∵当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
故③错误;
∵抛物线 ![]() 与x轴交于点(-3,0),其对称轴为直线
与x轴交于点(-3,0),其对称轴为直线![]() ,
,
∴抛物线 ![]() 与x轴交于点(-3,0)和(2,0),
与x轴交于点(-3,0)和(2,0),
∴![]() 的两根是:
的两根是:![]() ,
,
∴![]() 的两根是:
的两根是:![]() ,
,
∵![]() 与
与![]() 的解相同,
的解相同,
∴![]() 的两根分别为
的两根分别为![]() ,
,
故④正确;
∵抛物线 ![]() 与x轴交于点(-3,0)和(2,0),
与x轴交于点(-3,0)和(2,0),
∴![]() =
=![]() ,
,
∵![]() (
(![]() )为方程
)为方程![]() 的两个根,
的两个根,
∴![]() (
(![]() )为方程
)为方程![]() 的两个根,
的两个根,
∴![]() (
(![]() )为抛物线
)为抛物线![]() =
=![]() 和直线y=-3的两个交点的横坐标,
和直线y=-3的两个交点的横坐标,
结合图象得:m<-3且n>2
故⑤错误;
故选A.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
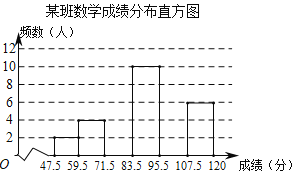
三点一测快乐周计划系列答案【题目】某市为了解九年级学生数学模拟考试成绩情况,随机抽取部分学生的成绩进行分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5~59.5 | 2 | 0.05 |
2 | 59.5~71.5 | 4 | 0.10 |
3 | 71.5~83.5 | a | 0.2 |
4 | 83.5~95.5 | 10 | 0.25 |
5 | 95.5~107.5 | b | c |
6 | 107.5~120 | 6 | 0.15 |
合计 | d | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ,d= ;
(2)补充完整频数分布直方图.
(3)已知全市九年级共有3500名学生参加考试,成绩96分及以上为优秀,估计全市九年级学生数学模拟考试成绩为优秀的学生人数是多少?