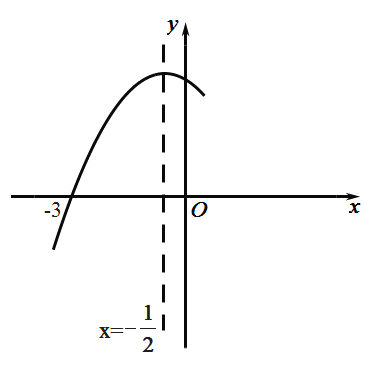Question

【题目】在平面直角坐标系中，抛物线与x轴交于点A,B ( A在B的左侧)

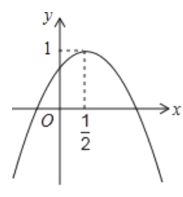
(1)如图1，若抛物线的对称轴为直线 .

①点A的坐标为( ， )，点B的坐标为( ， );

②求抛物线的函数表达式;

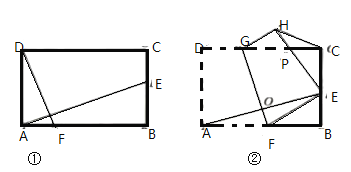
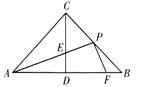
(2)如图2，将(1)中的抛物线向右平移若干个单位，再向下平移若干个单位，使平移后的抛物线经过点O，且与x正半轴交于点C，记平移后的抛物线顶点为P，若是等腰直角三角形，求点P的坐标.

Answer 1

【答案】（1）①A（-5,0），B（-1,0）；②；（2）P（1,1）；

【解析】

（1）①由抛物线的对称轴为直线 ，即可得到A，B的坐标；②根据待定系数法，即可求解；

（2）设平移后的抛物线的解析式为：，（b>0），可得：点C的坐标是（b，0），点P的坐标是（，），根据是等腰直角三角形，列出关于b的方程，即可求解.

（1）①∵抛物线与x轴交于点A，B，对称轴为直线 ，

∴点A(-5，0)，点B(-1，0)；

②把A(-5，0)，B(-1，0)代入，

得：，解得：，

∴抛物线的函数表达式是：；

（2）∵平移后的抛物线经过点O，

∴设平移后的抛物线的解析式为：，（b>0），

∴点C的坐标是（b，0），点P的坐标是（，），

∵是等腰直角三角形，

∴=，解得：b=2或b=0（舍去），

∴点P的坐标是：（1，1）.