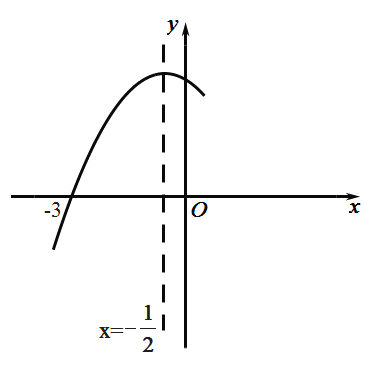题目内容
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
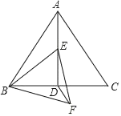
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
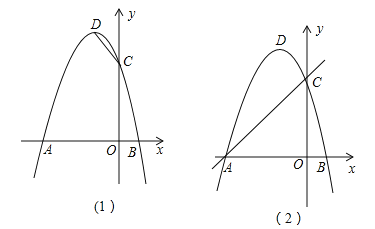
【答案】(1)A(﹣3,0),C(0,3),D(﹣1,4);(2)E(![]() ,0);(3)P(2,﹣5)或(1,0).
,0);(3)P(2,﹣5)或(1,0).
【解析】
试题(1)令抛物线解析式中y=0,解关于x的一元二次方程即可得出点A、B的坐标,再令抛物线解析式中x=0求出y值即可得出点C坐标,利用配方法将抛物线解析式配方即可找出顶点D的坐标;
(2)作点C关于x轴对称的点C′,连接C′D交x轴于点E,此时△CDE的周长最小,由点C的坐标可找出点C′的坐标,根据点C′、D的坐标利用待定系数法即可求出直线C′D的解析式,令其y=0求出x值,即可得出点E的坐标;
(3)根据点A、C的坐标利用待定系数法求出直线AC的解析式,假设存在,设点F(m,m+3),分∠PAF=90°、∠AFP=90°和∠APF=90°三种情况考虑.根据等腰直角三角形的性质结合点A、F点的坐标找出点P的坐标,将其代入抛物线解析式中即可得出关于m的一元二次方程,解方程求出m值,再代入点P坐标中即可得出结论.
试题解析:(1)当![]() 中y=0时,有
中y=0时,有![]() ,解得:
,解得:![]() =﹣3,
=﹣3,![]() =1,∵A在B的左侧,∴A(﹣3,0),B(1,0).
=1,∵A在B的左侧,∴A(﹣3,0),B(1,0).
当![]() 中x=0时,则y=3,∴C(0,3).
中x=0时,则y=3,∴C(0,3).
∵![]() =
=![]() ,∴顶点D(﹣1,4).
,∴顶点D(﹣1,4).
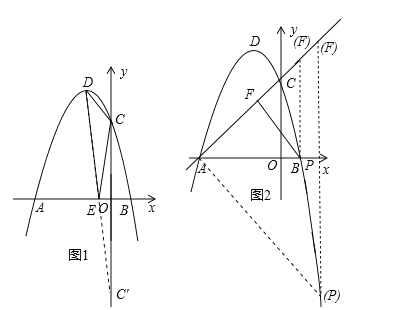
(2)作点C关于x轴对称的点C′,连接C′D交x轴于点E,此时△CDE的周长最小,如图1所示.
∵C(0,3),∴C′(0,﹣3).
设直线C′D的解析式为y=kx+b,则有:![]() ,解得:
,解得:![]() ,∴直线C′D的解析式为y=﹣7x﹣3,当y=﹣7x﹣3中y=0时,x=
,∴直线C′D的解析式为y=﹣7x﹣3,当y=﹣7x﹣3中y=0时,x=![]() ,∴当△CDE的周长最小,点E的坐标为(
,∴当△CDE的周长最小,点E的坐标为(![]() ,0).
,0).
(3)设直线AC的解析式为y=ax+c,则有:![]() ,解得:
,解得:![]() ,∴直线AC的解析式为y=x+3.
,∴直线AC的解析式为y=x+3.
假设存在,设点F(m,m+3),△AFP为等腰直角三角形分三种情况(如图2所示):
①当∠PAF=90°时,P(m,﹣m﹣3),∵点P在抛物线![]() 上,∴
上,∴![]() ,解得:m1=﹣3(舍去),m2=2,此时点P的坐标为(2,﹣5);
,解得:m1=﹣3(舍去),m2=2,此时点P的坐标为(2,﹣5);
②当∠AFP=90°时,P(2m+3,0)
∵点P在抛物线![]() 上,∴
上,∴![]() ,解得:m3=﹣3(舍去),m4=﹣1,此时点P的坐标为(1,0);
,解得:m3=﹣3(舍去),m4=﹣1,此时点P的坐标为(1,0);
③当∠APF=90°时,P(m,0),∵点P在抛物线![]() 上,∴
上,∴![]() ,解得:m5=﹣3(舍去),m6=1,此时点P的坐标为(1,0).
,解得:m5=﹣3(舍去),m6=1,此时点P的坐标为(1,0).
综上可知:在抛物线上存在点P,使得△AFP为等腰直角三角形,点P的坐标为(2,﹣5)或(1,0).

【题目】已知抛物线y=x2﹣2x﹣3.
(1)抛物线与x的交点坐标是 ,顶点是 .
(2)选取适当的数据填入下表.在直角坐标系中利用五点法画出此抛物线的图象.
X | … | … | |||||
y | … | … |
(3)结合函数图象,回答下题:
若抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1<x2<1比较y1,y2的大小: .当y<0,自变量x的取值范围是 .
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 4 | … |
y | … | 10 | 1 | ﹣2 | 1 | 25 | … |
(1)求这个二次函数的解析式;
(2)写出这个二次函数图象的开口方向、对称轴和顶点坐标.