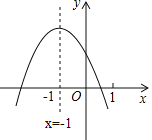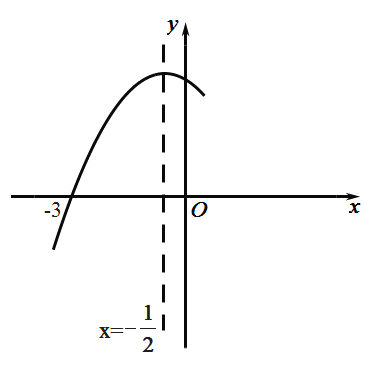ЬтФПФкШн
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2Љ2axЉ2ЃЈaЁй0ЃЉЃЎ
ЃЈ1ЃЉИУЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсЪЧжБЯпЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєИУЖўДЮКЏЪ§ЕФЭМЯѓПЊПкЯђЩЯЃЌЕБЉ1ЁмxЁм5ЪБЃЌКЏЪ§ЭМЯѓЕФзюИпЕуЮЊMЃЌзюЕЭЕуЮЊNЃЌЕуMЕФзнзјБъЮЊ![]() ЃЌЧѓЕуMКЭЕуNЕФзјБъЃЛ
ЃЌЧѓЕуMКЭЕуNЕФзјБъЃЛ
ЃЈ3ЃЉШєИУЖўДЮКЏЪ§ЕФЭМЯѓПЊПкЯђЯТЃЌЖдгкИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФСНЕуAЃЈx1ЃЌy1ЃЉЁЂBЃЈx2ЃЌy2ЃЉЃЌЕБx2Ён3ЪБЃЌОљгаy1Ёнy2ЃЌЧыНсКЯЭМЯѓЃЌжБНгаДГіx1ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉxЃН1ЃЛЃЈ2ЃЉMЃЈ5ЃЌ![]() ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛЃЈ3ЃЉЉ1Ёмx1Ём3
ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛЃЈ3ЃЉЉ1Ёмx1Ём3
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЖўДЮКЏЪ§НтЮіЪНЛЏЮЊyЃНax2Љ2axЉ2ЃНaЃЈxЉ1ЃЉ2ЉaЉ2ЃЌМДПЩЧѓЖдГЦжсЃЛ
ЃЈ2ЃЉгЩЬтвтПЩжЊaЃО0ЃЌЕБЉ1ЁмxЁм5ЪБЃЌxЃН5ЪБКЏЪ§газюДѓжЕЃЌЕБxЃН1ЪБКЏЪ§газюаЁжЕЃЌПЩШЗЖЈMЃЈ5ЃЌ![]() ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛ
ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛ
ЃЈ3ЃЉЧѓГіЕуЃЈ3ЃЌ0ЃЉЙигкxЃН1ЖдГЦЕФЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЌгЩЬтвтПЩжЊAЕФКсзјБъдкЉ1ЃЌ3жЎМфЪЧТњзуx2Ён3ЪБЃЌОљгаy1Ёнy2ЃЎ
НтЃКЃЈ1ЃЉyЃНax2Љ2axЉ2ЃНaЃЈxЉ1ЃЉ2ЉaЉ2ЃЌ
ЁрЖдГЦжсЮЊxЃН1ЃЌ
ЙЪД№АИЮЊxЃН1ЃЛ
ЃЈ2ЃЉЁпКЏЪ§ЕФПЊПкЯђЩЯЃЌ
ЁрaЃО0ЃЌ
ЕБЉ1ЁмxЁм5ЪБЃЌxЃН5ЪБКЏЪ§газюДѓжЕЃЌЕБxЃН1ЪБКЏЪ§газюаЁжЕЃЌ
ЁпзюИпЕуMЕФзнзјБъЪЧ![]() ЃЌ
ЃЌ
ЁрЕБxЃН5ЪБyЃН![]() ЃЌ
ЃЌ
ЁрaЃН2ЃЌ
ЁрMЃЈ5ЃЌ![]() ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛ
ЃЉЃЌNЃЈ1ЃЌЉ4ЃЉЃЛ
ЃЈ3ЃЉЁпКЏЪ§ЕФПЊПкЯђЯТЃЌ
ЁрaЃМ0ЃЌ
ЃЈ3ЃЌ0ЃЉЙигкxЃН1ЖдГЦЕФЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЌ
ЁпЕБx2Ён3ЪБЃЌОљгаy1Ёнy2ЃЌ
ЁрЉ1Ёмx1Ём3ЃЎ