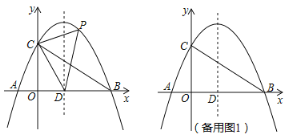
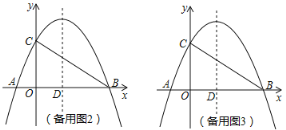
��Ŀ����
����Ŀ�����ڸ�������y��a1x2+b1x+c1������a1��b1��c1Ϊ��������a1��0������ƺ���y�� ��a1��a2��b1+b2��0��c1+c2��0��Ϊ����y��a1x2+b1x+c1������a1��b1��c1Ϊ��������a1��0��������غ�������������غ�������ͼ���ΪG��
��a1��a2��b1+b2��0��c1+c2��0��Ϊ����y��a1x2+b1x+c1������a1��b1��c1Ϊ��������a1��0��������غ�������������غ�������ͼ���ΪG��
��1����֪����y����x2+4x+2��
��ֱ��д���������������غ�������
������P��a��1��������غ�������ͼ���ϣ���a��ֵ��
����ֱ��y��m��ͼ��Gǡ�������������㣬ֱ��д��m��ȡֵ��Χ��
��2���躯��y����![]() x2+nx+1��n��0������غ�����ͼ��G�ک�4��x��2�ϵ���ߵ��������Ϊy0����
x2+nx+1��n��0������غ�����ͼ��G�ک�4��x��2�ϵ���ߵ��������Ϊy0����![]() ��y0��9ʱ��ֱ��д��n��ȡֵ��Χ��
��y0��9ʱ��ֱ��д��n��ȡֵ��Χ��
���𰸡���1����y��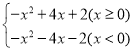 ����a��ֵΪ��3��1��2+
����a��ֵΪ��3��1��2+![]() ����m����2��2��m��6����2��1��n��2��n��
����m����2��2��m��6����2��1��n��2��n��![]()
��������
��1����ֱ����������غ������ó����ۣ�
����a��0��a��0��������غ�����ϵʽ�У����ɵó����ۣ�
����������ͼ��ֱ��д�����ۣ�
��2���ȵó�y����![]() x2+nx+1��n��0��������غ��������ٷ����������ͼ�ɵó����ۣ�
x2+nx+1��n��0��������غ��������ٷ����������ͼ�ɵó����ۣ�
�⣺��1����������غ������ó�y��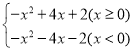 ��
��
�ڡ���P��a��1��������غ�������ͼ���ϣ�
��a��0ʱ����a2+4a+2��1��
��ã�a��2+![]() ��a��2��
��a��2��![]() ���ᣩ��
���ᣩ��
��a��0ʱ����a2��4a��2��1��
��ã�a����1��a����3��
����a��ֵΪ��3��1��2+![]() ��
��
����ͼ1��
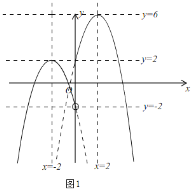
����֪��y��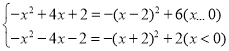 ��
��
��ֱ��y��m��ͼ��Gǡ�������������㣬
��ͼ��֪��m����2��2��m��6��
��2��������֪������y����![]() x2+nx+1��n��0��������غ�����Ϊy��
x2+nx+1��n��0��������غ�����Ϊy��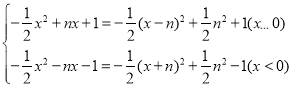 ��
��
��![]() n2+1��
n2+1��![]() n2��1��
n2��1��
����![]() n2��1��1ʱ����ͼ2��
n2��1��1ʱ����ͼ2��
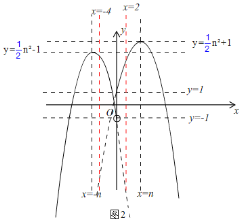
��n����2���ᣩ��n��2��
������n��4ʱ��
��x��2ʱ��y����4+2n+1��2n��3��
��x����4ʱ��y����8+4n��1��4n��9��
i����2n��3��4n��9��
��n��3��������������ڣ�
ii����2n��3��4n��9��
��n��3��
����n��4��
������2��n��4ʱ��
��x��2ʱ��y����4+2n+1��2n��3
i����2n��3��![]() n2��1��
n2��1��
����n��2��2��0�����������⣬
ii����2n��3��![]() n2��1��
n2��1��
����n��2��2��0��
��ʱ��y0��![]() n2��1��
n2��1��
��![]() ��y0��9��
��y0��9��
��![]() ��
��![]() n2��1��9��
n2��1��9��
��![]() ��n��2
��n��2![]() ��
��
����![]() ��n��4��
��n��4��
����0��n��2ʱ��
��ͼ3����![]() n2+1��
n2+1��![]() n2��1��
n2��1��
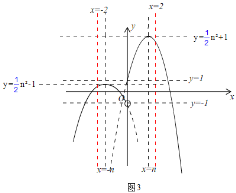
��![]() ��
��![]() n2+1��9��
n2+1��9��
��1��n��4��
��1��n��2��
����1��n��2��n��![]() ��
��

����Ŀ��ijˮ����˾����10 000kgƻ������˾��֪��ƻ��������,������ƻ���������ȡ���ɽ���ͳ�ƣ����ֽ�����±���
ƻ��������n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
��ƻ������m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
ƻ����Ƶ�� (�������С�������λ) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
��������ƻ���ĸ���Ϊ_____(�������С�����һλ)����ƻ��Լ��______kg��
����Ŀ��Ϊ���ﴫͳ�Ļ���ijУ��չ�������о����Ļ����Ķ��������������Ϊ�˽��ߡ����꼶ѧ��(�ߡ����꼶����600��ѧ��)���Ķ�Ч������У�����˾����Ļ�֪ʶ�������ִ������꼶�������ȡ20��ѧ���ľ����ɼ�(�ٷ���)���з������������£�
�ռ����ݣ�
���꼶��79��85��73��80��75��76��87��70��75��94��75��79��81��71��75��80��86��59��83��77��
���꼶��92��74��87��82��72��81��94��83��77��83��80��81��71��81��72��77��82��80��70��41��
�������ݣ�
|
|
|
|
|
| |
���꼶 | 0 | 1 | 0 | a | 7 | 1 |
���꼶 | 1 | 0 | 0 | 7 | b | 2 |
�������ݣ�
ƽ���� | ���� | ��λ�� | |
���꼶 | 78 | 75 |
|
���꼶 | 78 |
| 80.5 |
Ӧ�����ݣ�
(1)���ϱ���գ�a= ��b= ��c= ��d= ��
(2)���Ƹ�У�ߡ��������꼶ѧ���ڱ��ξ����гɼ���90�����ϵĹ��ж����ˣ�
(3)����Ϊ�ĸ��꼶��ѧ���Ծ����Ļ�֪ʶ���յ�����ˮƽ�Ϻã���˵�����ɣ�