题目内容
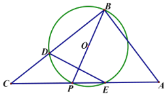
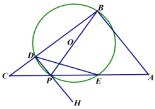
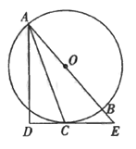
【题目】如图，AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E , 
交EC的延长线于点D，连接AC .
(1)求证: AC平分∠DAE ;
(2)若
，求⊙O的半径.
【答案】（1）详见解析；（2）4.
【解析】
(1)连接OC，由DE与⊙O相切与点C，得OC⊥EC，从而得OC∥AD，即∠DAC=∠OCA，结合∠OAC=∠OCA，即可得到结论；
(2)由∠DAE=∠COE，
，设OC=2x，则OC=3x，列出方程，即可求解.
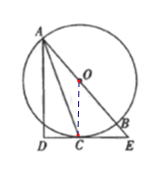
（1）连接OC，
∵DE与⊙O相切与点C，
∴OC⊥EC，
∵
，
∴OC∥AD，
∴∠DAC=∠OCA，
∵OC=OA，
∴∠OAC=∠OCA，
∴∠DAC=∠OAC，
∴AC平分∠DAE ；
（2）∵OC∥AD，
∴∠DAE=∠COE，
∴，
设OC=2x，则OC=3x，
∵OB=OC=2x，BE=2，
∴2x+2=3x，解得：x=2，
∴OC=2x=2×2=4，
∴⊙O的半径是4.
练习册系列答案
相关题目
