题目内容
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于A（﹣2，0），B（8，0）两点，与y轴交于点C，且OC＝2OA，抛物线的对称轴x轴交于点D．
（1）求抛物线的解析式；
（2）点P是第一象限内抛物线上位于对称轴右侧的一个动点，设点P点的横坐标为m，且S△CDP＝
S△ABC，求m的值；
（3）K是抛物线上一个动点，在平面直角坐标系中是否存在点H，使B、C、K、H为顶点的四边形成为矩形？若存在，直接写出点H的坐标；若不存在，说明理由．
【答案】（1）y＝﹣
x2+
x+4；（2）m1＝4或m2＝
；（3）点H坐标为（6，﹣4），（6，﹣2），（﹣18，﹣32）．
【解析】
（1）结合A（﹣2，0），B（8，0）由两点式可得抛物线解析式为y＝a（x+2）（x﹣8），求出点C坐标，代入即可求出抛物线解析式；
（2）点P在抛物线上，可设P（m，﹣m2+m+4），结合C点坐标可得直线PC的解析式，已知直线与对称轴交点E的坐标，DE长可知，根据S△ABC＝
×AB×OC求出其面积，由题中条件可知△CDP的面积，由三角形面积公式可得m的值；
（3）分类讨论，①若BC为边，∠CBK＝90°时，将BC绕点B逆时针旋转90°得到BC'，根据AAS证明△BCO≌△BC'E，依据全等的性质可得点B点C的坐标，求出直线BC的表达式与抛物线的解析式联立求解可得点K横坐标，由矩形的性质可知xC﹣xB＝xH﹣xK，
，结合点B、C、D点坐标可得H点坐标.②若BC为边，∠BCK＝90°时，同理可求：直线CK的解析式，与抛物线的解析式联立求解可得点K横坐标，同理可得H点坐标；③若BC为对角线，由B点C点坐标可得BC的中点坐标及BC的长，点K在抛物线上，设设点K（x，﹣x2+x+4），利用勾股定理可求出x的值，选择符合题意的，求出点K坐标后结合KH的中点坐标可知H点坐标，综上所述，点H的坐标有3种情况.
（1）∵A（﹣2，0），B（8，0）
∴OA＝2，OB＝8，
∵OC＝2OA，
∴OC＝4，
∴点C（0，4）
∵设y＝a（x+2）（x﹣8）经过点C，
∴4＝﹣16a，
∴a＝﹣，
∴抛物线解析式为：y＝﹣（x+2）（x﹣8）＝﹣x2+x+4；
（2）如图1，
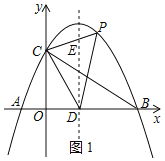
由题意：点D（3，0），
∴OD＝3，
设P（m，﹣m2+m+4），（m＞0，﹣m2+m+4＞0）
∵C（0，4），
∴直线PC的解析式可表示为：y＝（﹣m+）x+4，
设直线PC与对称轴的交点为E，则点E（3，﹣
m+
），
∴DE＝﹣m+，
∵S△ABC＝×AB×OC，
∴S△ABC＝×10×4＝20，
∵S△CDP＝
S△ABC，
∴×（﹣m+）×m＝×20，
∴m1＝4或m2＝；
（3）若BC为边，∠CBK＝90°时，如图2，将BC绕点B逆时针旋转90°得到BC'，
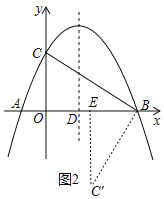
∴BC＝BC'，∠CBC'＝90°，
∴∠CBO+∠C'＝90°，∠CBO+∠OCB＝90°，
∴∠OCB＝∠EBC'，且BC＝BC'，∠BEC'＝∠BOC＝90°，
∴△BCO≌△BC'E（AAS）
∴BE＝OC＝4，OB＝EC'＝8，
∴点C'（4，﹣8），且B（8，0）
∴直线BC'解析式为：y＝2x﹣16，
∴2x﹣16＝﹣x2+x+4，
∴x1＝﹣10，x2＝8，
∴点K（﹣10，﹣36），
∵xC﹣xB＝xH﹣xK，
∴0﹣8＝xH﹣（﹣10），
∴xH＝﹣18，
∵，
∴yH＝﹣32，
∴点H（﹣18，﹣32），
若BC为边，∠BCK＝90°时，
同理可求：直线CK的解析式为：y＝2x+4，
∴2x+4＝﹣x2+x+4，
∴x1＝﹣2，x2＝0，
∴点K坐标（﹣2，0）
∵
，
∴0﹣8＝﹣2﹣xH，
∴xH＝﹣6，
∵，
∴yH＝﹣4，
∴点H（6，﹣4），
若BC为对角线，
∵B、C、K、H为顶点的四边形成为矩形，
∴BC＝KH，BC与KH互相平分，
∵B（8，0），C（0，4）
∴BC中点坐标（4，2），BC＝
＝
＝4
，
设点K（x，﹣x2+x+4）
∴（x﹣4）2+（﹣x2+x+4﹣2）2＝（2）2，
∴x（x﹣2）2（x﹣8）＝0，
∴x1＝0，x2＝2，x3＝8，
∴K（2，6），且KH的中点坐标（4，2），
∴点H（6，﹣2）
综上所述：点H坐标为（6，﹣4），（6，﹣2），（﹣18，﹣32）．
