��Ŀ����
����Ŀ�������ַ���֤����Բ���ڽ��ı��ζԽǻ�������
��֪����ͼ�٣��ı���ABCD�ڽ��ڡ�O��
��֤����B����D��180����
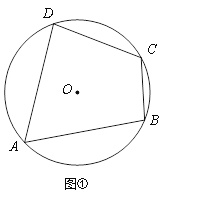

֤��1����ͼ�ڣ���ֱ��DE����O�ڵ�E������AE��CE��
��DE�ǡ�O��ֱ����
�� ��
�ߡ�DAE����AEC����DCE����ADC��360����
���AEC����ADC��360������DAE����DCE��360����90����90����180����
�ߡ�B�͡�AEC���ԵĻ���![]() ��
��
�� ��
���B����ADC��180����
���֤��1�������������ò�ͬ�ķ������֤��2��
֤��2��
���𰸡��������
��������
(1)����ֱ�����Ե�Բ�ܽ�Ϊ90�㼴�ɲ�ȫ֤�����̣�
��2������Բ�ܽ���Բ�ĽǵĹ�ϵ���ܽ�Ϊ360�㼴�����.
֤��1����ͼ������ֱ��DE����O�ڵ�E������AE��CE��
��DE����O��ֱ����
����DAE����DCE��90����
�ߡ�DAE����AEC����DCE����ADC��360����
���AEC����ADC��360������DAE����DCE��360����90����90����180����
�ߡ�B����AEC���ԵĻ���![]() ��
��
����AEC����B����
���B����ADC��180����

֤��2������OA��OC
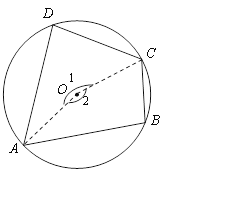
�ߡ�B����1���ԵĻ���![]() ��
��
��D����2���ԵĻ���![]() ��
��
���B��![]() ��1����D��
��1����D��![]() ��2
��2
�ߡ�1����2��360����
���B����D��![]() (��1����2)��
(��1����2)��![]() ��360����180����
��360����180����

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д�����Ŀ��Ϊ���ȫ�С���ֹ���սոѡ�������ijѧУ�����ˡ���ֹ���սոѣ�������������������Ϊ������ݽ�����. ������ί����������ͬѧ�ijɼ��������������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���ṩ����Ϣ������������⣺
������ ������Ϊx�֣� | Ƶ�� | �ٷֱ� |
60��x��70 | 8 | 20% |
70��x��80 | a | 30% |
80��x��90 | 16 | b% |
90��x��100 | 4 | 10% |
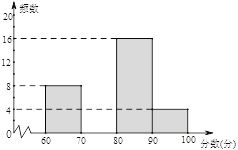
��1�����е�a�� ��b��������������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����������ͳ��ͼ�������ɼ��ֲ�������������70��x��80��Ӧ��Բ�ĽǵĶ����� ��
��4�������ɼ�������90�ֵ�4��ͬѧ��������2����ͬѧ��2��Ůͬѧ.ѧУ����4��ͬѧ�������ȡ2��ͬѧ���ܵ���̨���߲ɷã������б�����״ͼ�ķ��������ó鵽һ����ͬѧ��һ��Ůͬѧ�ĸ���.