题目内容
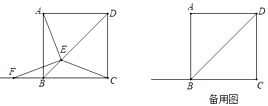
【题目】如图,已知等边三角形△ABC,点 D,E 分别在 CA,CB 的延长线上,且 BE=CD,O为 BC 的中点,MO⊥AB 交 DE 于点 M,OM=![]() ,AD=2,则 AB=________________.
,AD=2,则 AB=________________.
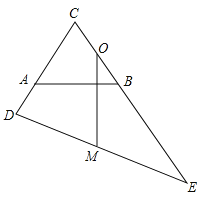
【答案】4
【解析】
先添加辅助线构造等腰三角形CFD,再推到O是EF中点,之后根据等腰三角形和等边三角形的性质来判断OM∥FD,之后判断出OM是三角形EFD的中位线即可求解本题.
解:如图,延长EC到点F,使CF=BE,
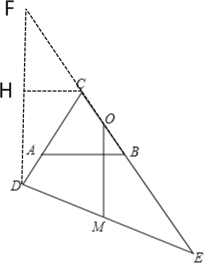
连接DF,
∵BE=CD,
∴CF=CD,
作CH⊥FD于H,
则H为FD的中点,
即FD=2FH,
∵![]() ABC是等边三角形,
ABC是等边三角形,
∴∠ACB=60°,
∴∠F=∠FDC=30°,
设![]() ABC的边长为4a,
ABC的边长为4a,
则CF=CD=2+4a,CE=4a+4a+2=8a+2,
∵O是BC中点,
∴OC=OB=2a,
∴OF=OE=6a+2,
故O为EF中点,
∵MO⊥AB 交 DE 于点 M,
∴∠BOM=30°=∠F,
∴OM∥FD,
故M为ED中点,
∴![]() ,
,
故![]() ,
,
在直角![]() CHF中,
CHF中,
∵CF=4a+2,∠F=30°,
∴CH=2a+1,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AB=4a=4;
故答案为:4.

练习册系列答案
相关题目