题目内容
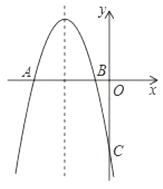
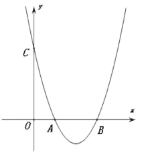
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
【答案】(1)作图见解析;(2)y=x2﹣4x+3;(3)3![]() .
.
【解析】
(1)利用基本作图,作AB的垂直平分线即可;
(2)根据等腰直角三角形的性质得到OB=OC=3,则C(0,3),B(3,0),然后利用待定系数法求抛物线解析式;
(3)连接BC交直线l于P,如图,根据两点之间线段最短可判断此时PC+PA的值最小,然后根据等腰直角三角形的性质计算出BC即可.
(1)如图,直线l为所作;
(2)∵△OBC是等腰直角三角形,且其腰长为3,即OB=OC=3,∴C(0,3),B(3,0),把C(0,3),B(3,0)分别代入y=x2+mx+n得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为y=x2﹣4x+3;
,∴抛物线解析式为y=x2﹣4x+3;
(3)连接BC交直线l于P,如图,则PA=PB.
∵PC+PA=PC+PB=BC,∴此时PC+PA的值最小,而BC=![]() OB=3
OB=3![]() ,∴PA+PC的最小值为3
,∴PA+PC的最小值为3![]() .
.
故答案为:3![]() .
.

练习册系列答案
相关题目
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④