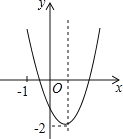题目内容
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售单价每涨价1元,月销售量就减少10千克.
(1)①求出月销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
②求出月销售利润w(元)与销售单价x(元/千克)之间的函数关系式;
(2)在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少元?
(3)当销售单价定为多少元时,能获得最大利润?最大利润是多少元?
【答案】(1)①y=﹣10x+1000;②w=﹣10x2+1400x﹣40000;(2)不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为80元;(3)售价定为70元时会获得最大利润,最大利润是9000元
【解析】
(1)根据题意可以得到月销售利润w(单位:元) 与售价x(单位:元/千克)之间的函数解析式;
(2)根据题意可以得到方程和相应的不等式,从而可以解答本题;
(3)根据(1)中的关系式化为顶点式即可解答本题.
解:(1)①由题意可得:y=500﹣(x﹣50)×10=﹣10x+1000;
②w=(x﹣40)[﹣10x+1000]=﹣10x2+1400x﹣40000;
(2)设销售单价为a元,
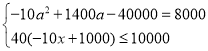 ,
,
解得,a=80,
答:商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为80元;
(3)∵y=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∴当x=70时,y取得最大值,此时y=9000,
答:当售价定为70元时会获得最大利润,最大利润是9000元;

【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④