题目内容
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
【答案】(1)y=![]() +2(x≠1);(2)见解析;(3)图象见解析;x≥2或0≤x<1;.
+2(x≠1);(2)见解析;(3)图象见解析;x≥2或0≤x<1;.
【解析】
(1)分别把两组数代入y=![]() +b得到方程组,求出a,b即可;
+b得到方程组,求出a,b即可;
(2)利用描点法画出图象即可;
(3)利用图象即可解决问题.
解:(1)把x=2时,y=4;x=﹣1时,y=1代入y=![]() +b得
+b得
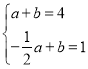 ,
,
解得![]() ,
,
∴该函数的解析式为y=![]() +2(x≠1);
+2(x≠1);
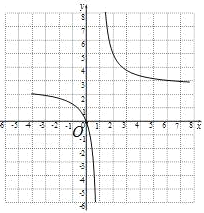
(2)如图:
(3)如图:在平面直角坐标系中作直线y=2x,
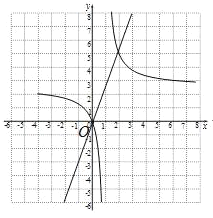
![]() 的图象与直线y=2x的交点为(0,0),(2,4),结合函数图象可得
的图象与直线y=2x的交点为(0,0),(2,4),结合函数图象可得![]() 的解集为x≥2或0≤x<1。
的解集为x≥2或0≤x<1。
故答案为:x≥2或0≤x<1

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.