题目内容
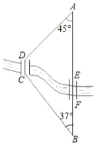
【题目】如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
(1)求证:CE=EF;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求△BEF面积的最大值.
【答案】(1)见解析;(2)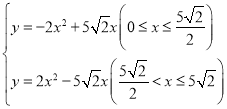 ;(3)50
;(3)50
【解析】
(1)作辅助线,构建三角形全等,证明△AEM≌△EFN和△ADE≌△CDE(SAS),可得AE=CE=EF;
(2)分两种情况:根据三角形的面积公式可得y与x之间关系的函数表达式,根据勾股定理计算BD的长可得x的取值;
(3)根据(2)中的两种情况,分别利用配方法和二次函数的增减性可得结论.
(1)证明:过E作MN∥AB,交AD于M,交BC于N,
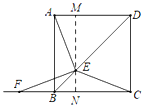
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:BD=![]() ,
,
∴0≤x≤5![]() ,
,
由题意得:BE=2x,
∴BN=EN=![]() x,
x,
由(1)知:△AEM≌△EFN,
则AE=EF=EC,
分两种情况:
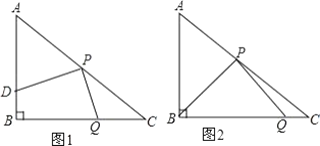
当0≤x≤ ![]() 时,如图1,
时,如图1,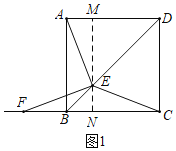
∵AB=MN=10,
∴ME=FN=10﹣![]() x,
x,
∴BF=FN﹣BN=10﹣![]() x﹣
x﹣![]() x=10﹣2
x=10﹣2![]() x,
x,
∴y=![]() =﹣2x2+5
=﹣2x2+5![]() x(0≤x≤
x(0≤x≤![]() );
);
当![]() 时,如图2,过E作EN⊥BC于N,
时,如图2,过E作EN⊥BC于N,
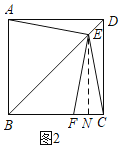
∴EN=BN=![]() x,
x,
∴FN=CN=10-![]() x,
x,
∴BF=BC-2CN=10-2(10-![]() x)=
x)=![]() x-10,
x-10,
∴y=![]() =2x2-5
=2x2-5![]() x(
x(![]() );
);
综上,y与x之间关系的函数表达式为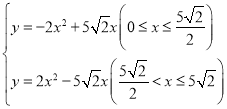
(3)①当0≤x≤ ![]() 时,如图1,
时,如图1,
∴y=﹣2x2+5![]() x=﹣2(x﹣
x=﹣2(x﹣![]() )2+
)2+![]() ,
,
∵﹣2<0,
∴当x=![]() 时,y有最大值是
时,y有最大值是![]() ;
;
当![]() 时,如图2,
时,如图2,
∴y=﹣2x2+5![]() x=2(x﹣
x=2(x﹣![]() )2-
)2-![]() ,
,
∵2>0,
∴当x=![]() 时,y有最大值是50;
时,y有最大值是50;
即△BEF面积的最大值是50.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案