题目内容
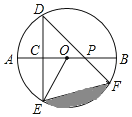
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
【答案】(1)![]() ;(2)
;(2)![]() π﹣
π﹣![]() .
.
【解析】
(1)根据垂径定理得CE的长,再根据已知DE平分AO得CO=![]() AO=
AO=![]() OE,根据勾股定理列方程求解.
OE,根据勾股定理列方程求解.
(2)先求出扇形的圆心角,再根据扇形面积和三角形的面积公式计算即可.
解:(1)连接OF,
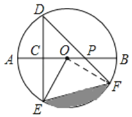
∵直径AB⊥DE,
∴CE=![]() DE=1.
DE=1.
∵DE平分AO,
∴CO=![]() AO=
AO=![]() OE.
OE.
设CO=x,则OE=2x.
由勾股定理得:12+x2=(2x)2.
x=![]() .
.
∴OE=2x=![]() .
.
即⊙O的半径为![]() .
.
(2)在Rt△DCP中,
∵∠DPC=45°,
∴∠D=90°﹣45°=45°.
∴∠EOF=2∠D=90°.
∴S扇形OEF=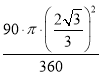 =
=![]() π.
π.
∵∠EOF=2∠D=90°,OE=OF=![]()
SRt△OEF=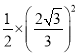 =
=![]() .
.
∴S阴影=S扇形OEF﹣SRt△OEF=![]() π﹣
π﹣![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目