题目内容
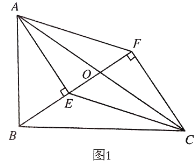
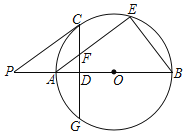
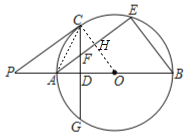
【题目】如图,AB为⊙O的直径,AE是⊙O的弦,C是弧AE的中点,弦CG⊥AB于点D,交AE于点F,过点C作⊙O的切线,交BA延长线于点P,连接BE
(1)求证:PC∥AE;
(2)若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
【答案】(1)详见解析;(2)BE=12.
【解析】
(1)连接OC,如图,先利用切线的性质得OC⊥PC,再利用垂径定理得到OC⊥AE,所以PC∥AE;
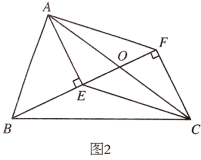
(2)设OC与AE交于点H,如图,利用垂径定理得到![]() ,根据圆周角定理得∠ACG=∠CAE,则AF=CF=5,在Rt△ADF中利用三角函数的定义可计算出DF=3,AD=4,再证明△OAH≌△OCD得到AH=CD=8,所以AE=2AH=16,然后证明Rt△ADF∽Rt△AEB,于是利用相似比可计算出BE.
,根据圆周角定理得∠ACG=∠CAE,则AF=CF=5,在Rt△ADF中利用三角函数的定义可计算出DF=3,AD=4,再证明△OAH≌△OCD得到AH=CD=8,所以AE=2AH=16,然后证明Rt△ADF∽Rt△AEB,于是利用相似比可计算出BE.
解:(1)证明:连接OC,如图,
∵PC为⊙O的切线,
∴OC⊥PC,
∵C是弧AE的中点,
∴OC⊥AE,
∴PC∥AE;
(2)设OC与AE交于点H,如图,
∵CG⊥AB,
∴![]() ,
,
∴![]() ,
,
∴∠ACG=∠CAE,
∴AF=CF=5,
∵PC∥AE,
∴∠EAB=∠P,
在Rt△ADF中,
∵sin∠P=sin∠FAD=![]() =
=![]() ,
,
∴DF=3,AD=4,
在△OAH和△OCD中,
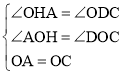 ,
,
∴△OAH≌△OCD(AAS),
∴AH=CD=5+3=8,
∴AE=2AH=16,
∵∠DAF=∠EAB,
∴Rt△ADF∽Rt△AEB,
∴DF:BE=AD:AE,即3:BE=4:16,
∴BE=12.

 考前必练系列答案
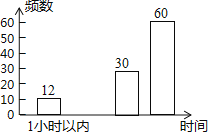
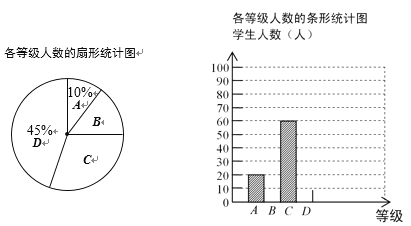
考前必练系列答案【题目】某市教育主管部门为了解学生的作业量情况,随机抽取了几所中学八年级的部分学生进行了一次调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图、表中所提供的信息解答下列问题:
(1)本次共抽取了 名学生进行调查;
(2)x= ,y= ,补全条形统计图;
(3)若这几所中学八年级的学生共有3200人,请估计做作业时间在2小时以上的学生人数是多少?
(4)由图表可知,这次被调查的八年级学生的作业时间的中位数一定落在1.5小时﹣2小时这一时段内,你认为这种判断正确吗?(不需要说明理由)
写作业时间 | 频数 | 频率 |
1小时以内 | 12 | 0.1 |
1﹣1.5 | x | 0.15 |
1.5﹣2 | 30 | 0.25 |
2小时以上 | 60 | y |