题目内容
【题目】如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
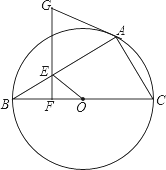
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)连接OA,由OA=OB,GA=GE得出∠ABO=∠BAO,∠GEA=∠GAE;再由EF⊥BC,得出∠BFE=90°,进一步由∠ABO+∠BEF=90°,∠BEF=∠GEA,最后得出∠GAO=90°求得答案;
(2)BC为直径得出∠BAC=90°,利用勾股定理得出BC=10,由△BEF∽△BCA,求得EF、BF的长,进一步在△OEF中利用勾股定理得出OE的长即可.
试题解析:(1)证明:如图,
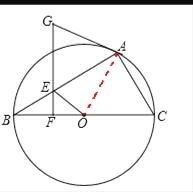
连接OA,
∵OA=OB,GA=GE
∴∠ABO=∠BAO,∠GEA=∠GAE
∵EF⊥BC,
∴∠BFE=90°,
∴∠ABO+∠BEF=90°,
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF,
∴∠BAO+∠GAE=90°,
即AG与⊙O相切.
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴![]()
∴EF=1.8,BF=2.4,
∴0F=0B-BF=5-2.4=2.6,
∴OE=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目