题目内容
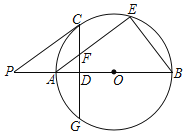
【题目】在△ABC中,点O是边AC的中点,分别过点A、C作射线BO的垂线,E、F是垂足.
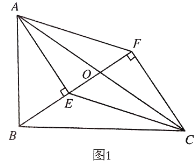
(1)如图1,求证:四边形AECF是平行四边形;
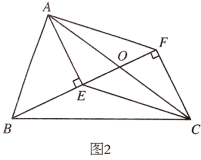
(2)如图2,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)CF=2.
【解析】
(1)根据AAS先证明△AOE≌△COF,从而得出EO=FO,结合AO=CO即可得出结论;
(2)先根据已知求出AO,CO的长,过点B作BH⊥AC于点H,在Rt△BCH中,根据![]() ,
,![]() 结合勾股定理可得出BH,CH的长,进而可求出HO的长.再在Rt△BOH中,可得出tan∠BOH=
结合勾股定理可得出BH,CH的长,进而可求出HO的长.再在Rt△BOH中,可得出tan∠BOH=![]() ,从而在Rt△AEO中,tan∠AOE=tan∠BOH=
,从而在Rt△AEO中,tan∠AOE=tan∠BOH=![]() ,结合AO的长,可以求出AE的长,由CF=AE可得出结果.
,结合AO的长,可以求出AE的长,由CF=AE可得出结果.
(1)证明:∵O为AC的中点,∴AO=CO.
又AE⊥BO,CF⊥BO,∴∠AEO=∠CFO=90°,
又∠AOE=∠FOC,∴△AOE≌△COF(AAS),
∴EO=FO,
又AO=CO,
∴四边形AECF是平行四边形;
(2)解:∵AC=BC![]() ,
,
∴AO=CO=![]() AC=
AC=![]() .
.
过点B作BH⊥AC于点H,
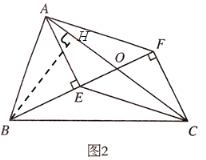
在Rt△BCH中,tan∠BCH=![]() ,
,
设BH=3x,则CH=4x,∴BC=![]() =5x=
=5x=![]() ,
,
∴x=![]() ,∴BH=
,∴BH=![]() ,CH=
,CH=![]() ,
,
∴HO=HC-OC=![]() ,
,
在Rt△BOH中,tan∠BOH=![]() ,
,
在Rt△AEO中,tan∠AOE=tan∠BOH=![]() ,
,
设OE=y,则AE=2y,AO![]() =
=![]() ,
,
∴y=1,∴AE=2,
又由(1)知四边形AECF是平行四边形,
∴CF=AE=2.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目