ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
ЮвУЧжЊЕР|x|ЕФМИКЮвтвхЪЧЃКдкЪ§жсЩЯЪ§xЖдгІЕФЕугыдЕуOЕФОрРыЃЌетИіНсТлПЩвдЭЦЙуЮЊЃК|x1Љx2|БэЪОдкЪ§жсЩЯЪ§x1ЃЌx2ЖдгІЕужЎМфЕФОрРыЃЎ
Р§ЃКНтЗНГЬ|xЉ1|+|x+2|ЃН5ЃЎ
гЩОјЖджЕЕФМИКЮвтвхжЊЃЌИУЗНГЬБэЪОЃКЧѓдкЪ§жсЩЯгы1КЭЉ2ЕФОрРыжЎКЭЮЊ5ЕФЕуЖдгІЕФЪ§ЃЌЖјдкЪ§жсЩЯЃЌ1КЭЉ2ЕФОрРыЮЊ|1ЉЃЈЉ2ЃЉ|ЃН3ЃЌТњзуЗНГЬЕФxЖдгІЕудк1ЕФгвБпЛђЉ2ЕФзѓБпЃЌШєxЖдгІЕудк1ЕФгвБпЃЌ
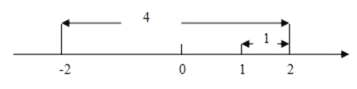
гЩЭМПЩжЊПДГіxЃН2ЃЛЭЌРэЃЌШєxЖдгІЕудкЉ2ЕФзѓБпЃЌПЩЕУxЃНЉ3ЃЌЙЪдЗНГЬЕФНтЪЧxЃН2ЛђxЃНЉ3ЃЎ
ВЮПМдФЖСВФСЯЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЗНГЬ|xЉ2|+|x+3|ЃН7ЕФНтЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉДњЪ§ЪН|xЉ1|+|x+4|ЕФзюаЁжЕЮЊЁЁ ЁЁЃЎ
ЃЈ3ЃЉШчЭМЃЌЕуAЁЂBЁЂCЪЧЪ§жсЩЯЕФШ§ЕуЃЌAЕуБэЪОЪ§ЪЧ-3ЃЌBЕуБэЪОЪ§ЪЧ-1ЃЌCЕуБэЪОЪ§ЪЧ6ЃЌЕуAЃЌBЃЌCПЊЪМдкЪ§жсЩЯдЫЖЏЃЌШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌМйЩшtУыжгЙ§КѓЃЌШєЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЌЕуAгыЕуCжЎМфЕФОрРыБэЪОЮЊACЃЌЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЎдђABЃНЁЁ ЁЁЃЌACЃНЁЁ ЁЁЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
![]()
ЃЈ4ЃЉдкЃЈ3ЃЉЕФЬѕМўЯТЃЌШєmACЉ4ABЕФжЕВЛЫцзХЪБМфtЕФБфЛЏЖјИФБфЃЌЪдШЗЖЈmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉx=-4Лђx=3ЃЛЃЈ2ЃЉ5ЃЛЃЈ3ЃЉ3t+2ЃЌ 9+4tЃЛЃЈ4ЃЉmЃН3
ЁОНтЮіЁП
ЃЈ1ЃЉЗжРрЬжТлЃК![]() ЃЌИљОнОјЖджЕЕФвтвхЃЌПЩЛЏМђЗНГЬЃЌШЛКѓНтЗНГЬЃЌПЩЕУД№АИЃЛ
ЃЌИљОнОјЖджЕЕФвтвхЃЌПЩЛЏМђЗНГЬЃЌШЛКѓНтЗНГЬЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉДњЪ§ЪН|xЉ1|+|x+4|ЕФзюаЁжЕМДЮЊxдк1КЭ-4жЎМфЪБжЕзюаЁЃЛ
ЃЈ3ЃЉИљОнЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌБэЪОГівЦЖЏЕФОрРыЃЌМДПЩЕУГіABЁЂACЃЛ
ЃЈ4ЃЉИљОнmACЉ4ABЕФжЕВЛЫцзХЪБМфtЕФБфЛЏЖјИФБфЃЌПЩвдХаЖЯГіКЙtЕФЯюЕФЯЕЪ§ЮЊ0,НјЖјФмЧѓГіmЕФжЕ.
ЕБ![]() ЪБЃЌдЗНГЬПЩЛЏЮЊ
ЪБЃЌдЗНГЬПЩЛЏЮЊ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌдЗНГЬЕШМлгк
ЪБЃЌдЗНГЬЕШМлгк![]() ЃЌВЛДцдкxЕФжЕЃЛ
ЃЌВЛДцдкxЕФжЕЃЛ
ЕБ![]() ЪБЃЌдЗНГЬЕШМлгк
ЪБЃЌдЗНГЬЕШМлгк![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ![]() Лђ
Лђ![]()
ДњЪ§ЪН|xЉ1|+|x+4|ЕФзюаЁжЕМДЮЊxдк1КЭ-4жЎМфЪБЕФжЕ
МДЮЊ![]() ЃЌ
ЃЌ
Ёр![]()
ЙЪД№АИЮЊ![]() .
.
ЃЈ3ЃЉЁпAЕуБэЪОЪ§ЪЧ-3ЃЌBЕуБэЪОЪ§ЪЧ-1ЃЌCЕуБэЪОЪ§ЪЧ6ЃЌ
Ёр![]() дРДЕФОрРыЪЧЃК
дРДЕФОрРыЪЧЃК![]() ЃЌ
ЃЌ![]() дРДЕФОрРыЪЧЃК
дРДЕФОрРыЪЧЃК![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЙЪЬюЃК![]() ЁЂ
ЁЂ![]()
ЃЈ4ЃЉЁпmACЉ4ABЃНmЃЈ4t+9ЃЉЉ4ЃЈ3t+2ЃЉЃНЃЈ4mЉ12ЃЉt+9mЉ8ЃЌ
ЁпmACЉ4ABЕФжЕВЛЫцзХЪБМфtЕФБфЛЏЖјИФБфЃЌ
Ёр4mЉ12ЃН0ЃЌ
ЁрmЃН3ЃЎ

ЁОЬтФПЁПЮЊЩљдЎбяжнЁАдЫКгЩъвХЁБЃЌФГаЃОйАьСЫвЛДЮдЫКгжЊЪЖОКШќЃЌТњЗж10ЗжЃЌбЇЩњЕУЗжЮЊећЪ§ЃЌГЩМЈДяЕН6ЗжвдЩЯЃЈАќРЈ6ЗжЃЉЮЊКЯИёЃЌДяЕН9ЗжвдЩЯЃЈАќКЌ9ЗжЃЉЮЊгХауЃЎетДЮОКШќжаМзввСНзщбЇЩњГЩМЈЗжВМЕФЬѕаЮЭГМЦЭМШчЭМЫљЪОЃЎ

ЃЈ1ЃЉВЙГфЭъГЩЯТУцЕФГЩМЈЭГМЦЗжЮіБэЃК
зщБ№ | ЦНОљЗж | жаЮЛЪ§ | ЗНВю | КЯИёТЪ | гХауТЪ |
Мззщ | 6.7 | 3.41 | 90% | 20% | |
ввзщ | 7.5 | 1.69 | 80% | 10% |
ЃЈ2ЃЉаЁУїЭЌбЇЫЕЃКЁАетДЮОКШќЮвЕУСЫ7ЗжЃЌдкЮвУЧаЁзщжаХХУћЪєжагЮТдЦЋЩЯЃЁЁБЙлВьЩЯБэПЩжЊЃЌаЁУїЪЧ зщЕФбЇЩњЃЛЃЈЬюЁАМзЁБЛђЁАввЁБЃЉ
ЃЈ3ЃЉМззщЭЌбЇЫЕЫћУЧзщЕФКЯИёТЪЁЂгХауТЪОљИпгкввзщЃЌЫљвдЫћУЧзщЕФГЩМЈКУгкввзщЃЎЕЋввзщЭЌбЇВЛЭЌвтМззщЭЌбЇЕФЫЕЗЈЃЌШЯЮЊЫћУЧзщЕФГЩМЈвЊКУгкМззщЃЎЧыФуИјГіСНЬѕжЇГжввзщЭЌбЇЙлЕуЕФРэгЩЃЎ




