题目内容
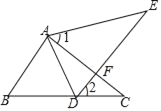
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OD,如图,根据圆周角定理得到∠AOD=2∠AED=90°,则OD⊥AB,再利用平行四边形的性质得CD∥AB,所以OD⊥CD,于是根据切线的判定定理得到CD是⊙O的切线;
(2)连结BE,通过圆周角定理将∠ADE的正弦值转化为∠ABE的正弦值.
试题解析:(1)证明:连结OD,如图,

∵∠AOD=2∠AED=2×45°=90°,
∴OD⊥AB,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)解:连结BE,
∵AB为直径,
∴∠AEB=90°,
根据圆周角定理:∠ADE=∠ABE,
∴sin∠ADE=sin∠ABE=![]() .
.
即∠DAE的正弦值是![]() .
.

练习册系列答案
相关题目
【题目】某商场销售一批进价为10元的新商品,为寻求合适的销售价格,他们进行了4天的试销,试销情况如下表:
第1天 | 第2天 | 第3天 | 第4天 | |
日销售单价x(元) | 20 | 30 | 40 | 50 |
日销售量y(个) | 300 | 200 | 150 | 120 |
(1)根据试销情况,请你猜测并求出y与x之间的函数关系式;
(2)若该商场计划每天销售这种商品的利润要达到3600元,问该商品销售单价应定为多少元?